
以直角坐標(biāo)系的原點O為極點,x軸的正半軸為極軸,且兩個坐標(biāo)系取相等的單位長度.已知直線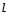 經(jīng)過點P(1,1),傾斜角
經(jīng)過點P(1,1),傾斜角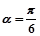 .
.
(1)寫出直線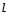 的參數(shù)方程;
的參數(shù)方程;
(2)設(shè)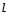 與圓
與圓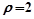 相交于兩點A、B,求點P到A、B兩點的距離之積.
相交于兩點A、B,求點P到A、B兩點的距離之積.
(1) (2)2
(2)2
【解析】本題考查了直線的參數(shù)方程、簡單曲線的極坐標(biāo)方程和直線與圓的位置關(guān)系等知識點,屬于中檔題.請同學(xué)們注意解題過程中用根與系數(shù)的關(guān)系,設(shè)而不求的思想方法.
(I)設(shè)出直線l上任意一點Q,利用直線斜率的坐標(biāo)公式可得到坐標(biāo)的關(guān)系:(y-1):(x-1)=1: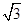 ,再令x-1=
,再令x-1=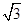 t,以t為參數(shù),可以得到直線l的參數(shù)方程;
t,以t為參數(shù),可以得到直線l的參數(shù)方程;
(II)將圓ρ=2化成普通方程,再與直線的參數(shù)方程聯(lián)解,得到一個關(guān)于t的一元二次方程.再用一元二次方程根與系數(shù)的關(guān)系,結(jié)合兩點的距離公式,可得出P到A、B兩點的距離之積.
解:(I)直線的參數(shù)方程是
 ---5分
---5分
(II)因為點A,B都在直線l上,所以可設(shè)它們對應(yīng)的參數(shù)為t1和t2,則點A,B的坐標(biāo)分別為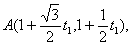
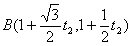 .
.
圓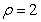 化為直角坐標(biāo)系的方程
化為直角坐標(biāo)系的方程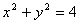 .
.
以直線l的參數(shù)方程代入圓的方程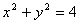 整理得到
整理得到
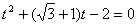 ①
①
因為t1和t2是方程①的解,從而t1t2=-2.
所以|PA|·|PB|= |t1t2|=|-2|=2. -----------------(12分)


 小題狂做系列答案
小題狂做系列答案科目:高中數(shù)學(xué) 來源: 題型:
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| π |
| 6 |
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 2 |
| π |
| 4 |
| 2π |
| 3 |
| x2 |
| 36 |
| y2 |
| 16 |
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
|
|
| π |
| 2 |
| π |
| 3 |
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com