
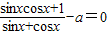 在
在 內恰有兩實數解,則實數a的取值范圍為 .
內恰有兩實數解,則實數a的取值范圍為 . 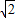 sin(x+
sin(x+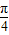 )=t,則得 t∈[-
)=t,則得 t∈[- ,0),a=
,0),a= =
= ,再利用基本不等式求出實數a的取值范圍.
,再利用基本不等式求出實數a的取值范圍.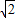 sin(x+
sin(x+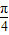 )=t,則有 sinxcosx=
)=t,則有 sinxcosx=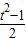 .
.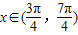 ,∴π≤x+
,∴π≤x+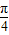 ≤2π,-1≤sin(x+
≤2π,-1≤sin(x+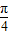 )≤0.
)≤0.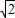 ,0),故
,0),故 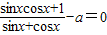 即
即 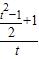 =a,即 a=
=a,即 a=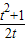 =
= .
.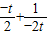 ≥2
≥2 =1,當且僅當
=1,當且僅當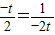 ,即 t=-1時,等號成立,故a≤-1,.
,即 t=-1時,等號成立,故a≤-1,.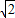 ,0)時,每一個t值,對應了滿足 π≤x+
,0)時,每一個t值,對應了滿足 π≤x+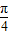 ≤2π 的2個x值(x+
≤2π 的2個x值(x+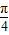 可能在第三象限,也可能在第四象限),
可能在第三象限,也可能在第四象限),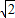 ,-1].
,-1].

 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com