
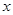 ,符號
,符號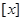 表示不超過
表示不超過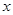 的最大整數,例如
的最大整數,例如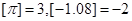 ,定義函數
,定義函數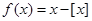 ,則下列命題中正確的是( )
,則下列命題中正確的是( )A.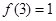 | B.方程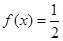 有且僅有一個解 有且僅有一個解 |
C.函數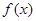 是周期函數 是周期函數 | D.函數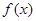 是增函數 是增函數 |
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
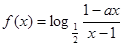 為奇函數,
為奇函數,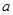 為常數,
為常數,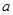 的值;
的值;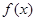 在區間
在區間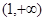 上單調遞增;
上單調遞增;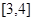 上的每一個
上的每一個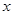 值,不等式
值,不等式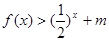 恒成立,求實數
恒成立,求實數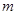 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
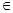 (0,π)恒成立?若存在,請求出a的范圍;若不存在,請說明理由.
(0,π)恒成立?若存在,請求出a的范圍;若不存在,請說明理由. 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
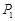 (元)和
(元)和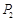 (元)分別記小王先后兩次買米時,該品種大米的單價,請問:僅這兩次買米而言,甲、乙兩種購買方式,從平均單價考慮,哪種比較合算?請進行探討,并給出探討過程.
(元)分別記小王先后兩次買米時,該品種大米的單價,請問:僅這兩次買米而言,甲、乙兩種購買方式,從平均單價考慮,哪種比較合算?請進行探討,并給出探討過程.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
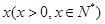 戶農民從事蔬菜加工,則剩下的繼續從事蔬菜種植的農民平均每戶的年收入有望提高
戶農民從事蔬菜加工,則剩下的繼續從事蔬菜種植的農民平均每戶的年收入有望提高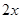 %,而從事蔬菜加工的農民平均每戶的年收入將為
%,而從事蔬菜加工的農民平均每戶的年收入將為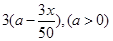 萬元.
萬元.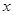 戶農民從事蔬菜加工后,要使從事蔬菜種植的農民的總年收入不低于動員前從事蔬菜種植的農民的總年收入,求
戶農民從事蔬菜加工后,要使從事蔬菜種植的農民的總年收入不低于動員前從事蔬菜種植的農民的總年收入,求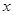 的取值范圍;
的取值范圍;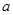 的最大值.
的最大值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 項目類別 | 年固定成本 | 每件產品成本 | 每件產品銷售價 | 每年最多可生產的件數 |
| A產品 | 10 | m | 5 | 100 |
| B產品 | 20 | 4 | 9 | 60 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com