
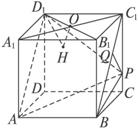
(1)求直線AP與平面BCC1B1所成的角的大小(結(jié)果用反三角函數(shù)值表示);
(2)設(shè)O點(diǎn)在平面D1AP上的射影是H,求證:D1H⊥AP;
(3)求點(diǎn)P到平面ABD1的距離.
解:如圖,(1)連結(jié)BP.

∵AB⊥平面BCC1B1,
∴AP與平面BCC1B1所成的角就是∠APB.
∵CC1=4CP,CC1=4,
∴CP=1.
在Rt△PBC中,∠PCB為直角,BC=4,CP=1,故BP=![]() .
.
在Rt△APB中,∠ABP為直角,tan∠APB=![]() ,
,
∴∠APB=arctan![]() ,
,
即直線AP與平面BCC1B1所成的角為arctan![]() .
.
(2)連結(jié)A1C1,B1D1.
∵四邊形A1B1C1D1是正主形,∴D1O⊥A1C1.
又AA1⊥底面A1B1C1D1,∴AA1⊥D1O.
∵AA1∩A1C1=A1,∴D1O⊥平面A1APC1.
∵AP![]() 平面A1APC1,∴D1O⊥AP.
平面A1APC1,∴D1O⊥AP.
∵平面D1AP的斜線D1O在這個(gè)平面內(nèi)的射影是D1H.∴D1H⊥AP.
(3)連結(jié)BC1,在平面BCC1B1中,過(guò)點(diǎn)P作PQ⊥BC1于點(diǎn)Q.
∵AB⊥平面BCC1B1,PQ![]() 平面BCC1B1,
平面BCC1B1,
∴PQ⊥AB.
∴PQ⊥平面ABC1D1.
∴PQ就是點(diǎn)P到平面ABD1的距離.
在Rt△C1PQ中,∠C1QP=90°,∠PC1Q=45°,PC1=3,
∴PQ=![]() ,即點(diǎn)P到平面ABD1的距離為
,即點(diǎn)P到平面ABD1的距離為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (2012•溫州一模)如圖,直線l⊥平面α,垂足為O,正四面體ABCD的棱長(zhǎng)為4,C在平面α內(nèi),B是直線l上的動(dòng)點(diǎn),則當(dāng)O到AD的距離為最大時(shí),正四面體在平面α上的射影面積為( )
(2012•溫州一模)如圖,直線l⊥平面α,垂足為O,正四面體ABCD的棱長(zhǎng)為4,C在平面α內(nèi),B是直線l上的動(dòng)點(diǎn),則當(dāng)O到AD的距離為最大時(shí),正四面體在平面α上的射影面積為( )查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
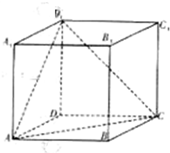 如圖,正方體ABCD-A1B1C1D1的棱長(zhǎng)為4,點(diǎn)P從B點(diǎn)出發(fā),在正方形BCC1B1的邊上按逆針?lè)较虬慈缦乱?guī)律運(yùn)動(dòng):設(shè)第n次運(yùn)動(dòng)的路程為an,且an=cos
如圖,正方體ABCD-A1B1C1D1的棱長(zhǎng)為4,點(diǎn)P從B點(diǎn)出發(fā),在正方形BCC1B1的邊上按逆針?lè)较虬慈缦乱?guī)律運(yùn)動(dòng):設(shè)第n次運(yùn)動(dòng)的路程為an,且an=cos| nπ | 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖,在正三棱柱ABC-A1B1C1中,點(diǎn)D,D1分別為棱BC,B1C1的中點(diǎn).
如圖,在正三棱柱ABC-A1B1C1中,點(diǎn)D,D1分別為棱BC,B1C1的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
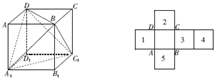 (2011•安徽模擬)下面關(guān)于棱長(zhǎng)為1的正方體ABCD-A1B1C1D1敘述正確的是
(2011•安徽模擬)下面關(guān)于棱長(zhǎng)為1的正方體ABCD-A1B1C1D1敘述正確的是
| ||
| 2 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年浙江省溫州市高三第一次適應(yīng)性測(cè)試?yán)砜茢?shù)學(xué) 題型:選擇題
如圖,直線 平面
平面 ,垂足為
,垂足為 ,正四面體
,正四面體 的棱長(zhǎng)為4,
的棱長(zhǎng)為4, 在平面
在平面 內(nèi),
內(nèi),
 是直線
是直線 上的動(dòng)點(diǎn),則當(dāng)
上的動(dòng)點(diǎn),則當(dāng) 到
到 的距離為最大時(shí),正四面體在平面
的距離為最大時(shí),正四面體在平面 上的射影面
上的射影面
積為( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com