
��֪�E�A �^(gu��)�c(di��n)
�^(gu��)�c(di��n)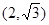 ���������x����
���������x����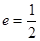 ��ֱ��
��ֱ��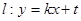 �c�E�A
�c�E�A ����
����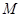 ��
��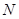 ���c(di��n)��
���c(di��n)��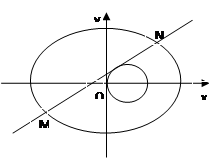
������E�A�Ę�(bi��o)��(zh��n)���̣�
����(d��ng)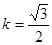 �r(sh��)�����C��
�r(sh��)�����C��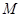 ��
��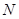 ���c(di��n)�ęM����(bi��o)��ƽ���͞鶨ֵ��
���c(di��n)�ęM����(bi��o)��ƽ���͞鶨ֵ��
������ֱ�� �c�A
�c�A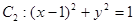 ���У��E�A��һ�c(di��n)
���У��E�A��һ�c(di��n)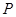 �M��
�M��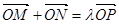 ����(sh��)��(sh��)
����(sh��)��(sh��)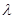 ��ȡֵ������
��ȡֵ������
(��)  ��
��
(��)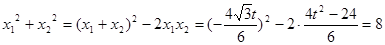 ���鶨ֵ��
���鶨ֵ��
����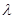 ��ȡֵ������
��ȡֵ������ 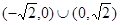 ��
��
����ԇ�}������(��) �O(sh��)�E�A�Ę�(bi��o)��(zh��n)���̞�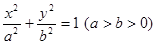
����֪�ã�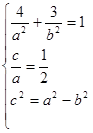 �����
����� 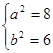
���ԙE�A�Ę�(bi��o)��(zh��n)���̞飺 4��
4��
(��) ��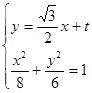 ����
����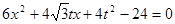 ���O(sh��)
���O(sh��) ��
��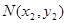 ��
��
�t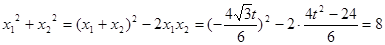 ���鶨ֵ�� 9��
���鶨ֵ�� 9��
������?y��n)�ֱ��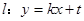 �c�A
�c�A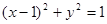 ����
����
���ԣ�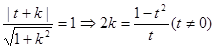
��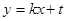 ����
���� �������ã�
�������ã�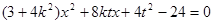
�O(sh��)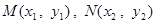 ���t��
���t�� 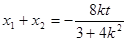
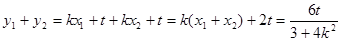
��?y��n)�?img src="http://thumb.zyjl.cn/pic5/tikupic/f1/b/9xtnm.png" style="vertical-align:middle;" />�� ���ԣ�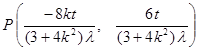
����?y��n)��c(di��n)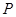 �ڙE�A�ϣ� ���ԣ�
�ڙE�A�ϣ� ���ԣ�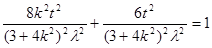
 �� ��?y��n)?
�� ��?y��n)?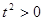 ����
���� 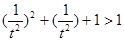 ��
��
���� 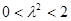 ������
������ 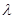 ��ȡֵ������
��ȡֵ������ 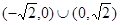 �� 16��
�� 16��
���c(di��n)�����}��Ҫ����E�A�Ę�(bi��o)��(zh��n)���̣��E�A�Ď����|(zh��)��ֱ���c�A���E�A��λ���P(gu��n)ϵ�����κ���(sh��)���|(zh��)��
�c(di��n)�u(p��ng)���Йn�}���漰�E�A���}Ŀ���ڽ�Щ��߿��}���nj�Ҋ(ji��n)���r�������漰���(bi��o)��(zh��n)���̣��о�ֱ���c�E�A��λ���P(gu��n)ϵ�����(bi��o)��(zh��n)���̣���Ҫ���]���x��a,b,c,e���P(gu��n)ϵ���漰ֱ���ڙE�Aλ���P(gu��n)ϵ��(w��n)�}��������(y��ng)���f�_(d��)�������漰ֱ���ڈA��λ���P(gu��n)ϵ��(w��n)�}���������á����������Ρ������}�ڑ�(y��ng)���f�_(d��)�����Ļ��A(ch��)�ϣ��õ�����(sh��)�ı��_(d��)ʽ����(y��ng)�ö��κ���(sh��)���|(zh��)ʹ��(w��n)�}�ý⡣


 ���������n�r(sh��)ͬ��Ӗ(x��n)��ϵ�д�
���������n�r(sh��)ͬ��Ӗ(x��n)��ϵ�д� �(y��ng)���n��ͬ������(x��)ϵ�д�
�(y��ng)���n��ͬ������(x��)ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ��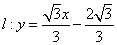 �^(gu��)�p����
�^(gu��)�p����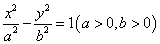 ��һ��(g��)���c(di��n)�����c�p������һ�l�u����ƽ��.
��һ��(g��)���c(di��n)�����c�p������һ�l�u����ƽ��.
�������p�����ķ��̣�
�������^(gu��)�c(di��n)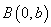 �c
�c �S��ƽ�е�ֱ���c�p�����ཻ�ڲ�ͬ�ă��c(di��n)
�S��ƽ�е�ֱ���c�p�����ཻ�ڲ�ͬ�ă��c(di��n) �Ĵ�ֱƽ�־���
�Ĵ�ֱƽ�־���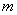 ����ֱ��
����ֱ��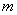 ��
��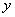 �S�Ͻؾ��ȡֵ����.
�S�Ͻؾ��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�ڙE�A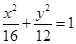 ����һ�c(di��n)��ʹ�@һ�c(di��n)��ֱ��
����һ�c(di��n)��ʹ�@һ�c(di��n)��ֱ��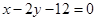 �ľ��x����Сֵ
�ľ��x����Сֵ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A�ăɂ�(g��)���c(di��n)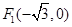 ��
��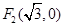 ���^(gu��)
���^(gu��)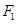 ���c����(bi��o)�S��ƽ�е�ֱ��
���c����(bi��o)�S��ƽ�е�ֱ��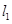 �c�E�A����
�c�E�A����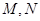 ���c(di��n)�����
���c(di��n)�����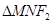 �����L(zh��ng)����8��
�����L(zh��ng)����8��
��1����E�A�ķ��̣�
��2�����^(gu��)�c(di��n)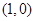 ��ֱ��
��ֱ��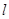 �c�E�A���ڲ�ͬ���c(di��n)
�c�E�A���ڲ�ͬ���c(di��n)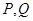 ��ԇ��(w��n)��
��ԇ��(w��n)��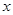 �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)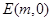 ��ʹ
��ʹ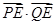 ��鶨ֵ�������ڣ�����c(di��n)
��鶨ֵ�������ڣ�����c(di��n)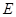 ������(bi��o)����ֵ;�������ڣ��f(shu��)�����ɡ�
������(bi��o)����ֵ;�������ڣ��f(shu��)�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����֪�E�AC��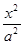 +
+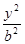 =1��a>b>0�������ҽ��c(di��n)�քe��F
=1��a>b>0�������ҽ��c(di��n)�քe��F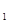 ��F
��F ��A�ǙE�AC�ϵ�һ�c(di��n)��AF
��A�ǙE�AC�ϵ�һ�c(di��n)��AF ��F
��F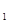 F
F ��O������(bi��o)ԭ�c(di��n)��OB��ֱAF
��O������(bi��o)ԭ�c(di��n)��OB��ֱAF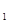 ��B����OF
��B����OF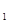 =3OB.
=3OB.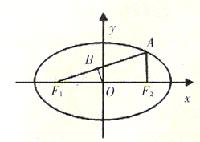
������E�AC���x���ʣ�
������t�ʣ�0��b����ʹ�����}���O(sh��)�Ax +y
+y =t
=t �������c(di��n)M��x
�������c(di��n)M��x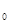 ��y
��y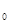 ��̎���о����E�AC��Q
��̎���о����E�AC��Q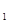 ��Q
��Q ���c(di��n)����ôOQ
���c(di��n)����ôOQ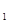 ��OQ
��OQ ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ������(bi��o)ϵ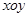 �У�����
�У�����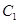 �ą���(sh��)���̞�
�ą���(sh��)���̞�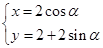 (
(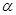 �酢��(sh��))
�酢��(sh��))  ��
��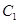 �ϵĄ�(d��ng)�c(di��n)��
�ϵĄ�(d��ng)�c(di��n)��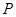 �c(di��n)�M��
�c(di��n)�M��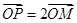 ��
��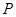 �c(di��n)��܉�E������
�c(di��n)��܉�E������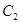 .
.
(1)��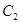 �ķ��̣�
�ķ��̣�
(2)���� ��O�c(di��n)��
��O�c(di��n)��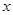 �S�������S��O�S�ĘO����(bi��o)ϵ�У��侀
�S�������S��O�S�ĘO����(bi��o)ϵ�У��侀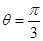 �c
�c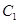 �Į��ژO�c(di��n)�Ľ��c(di��n)��
�Į��ژO�c(di��n)�Ľ��c(di��n)�� ���c
���c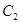 �Į��ژO�c(di��n)�Ľ��c(di��n)��
�Į��ژO�c(di��n)�Ľ��c(di��n)�� ����
����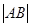 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�p����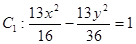 ���c(di��n)
���c(di��n)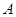 ��
��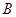 �քe���p����
�քe���p����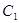 �����ҽ��c(di��n)����(d��ng)�c(di��n)
�����ҽ��c(di��n)����(d��ng)�c(di��n)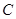 ��
�� �S�Ϸ�.
�S�Ϸ�.
��1�����c(di��n)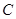 ������(bi��o)��
������(bi��o)��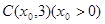 ���p������һ�l�u�����ϵ��c(di��n)������
���p������һ�l�u�����ϵ��c(di��n)������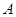 ��
��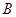 �齹�c(di��n)�ҽ�(j��ng)�^(gu��)�c(di��n)
�齹�c(di��n)�ҽ�(j��ng)�^(gu��)�c(di��n)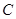 �ęE�A�ķ��̣�
�ęE�A�ķ��̣�
��2������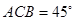 �����
�����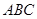 ����ӈA�ķ��̣�
����ӈA�ķ��̣�
��3�����ڽo��ֱ��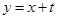 ����ȡһ�c(di��n)
����ȡһ�c(di��n)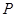 �����c(di��n)
�����c(di��n)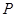 ��(2)�ЈA��һ�l�о������c(di��n)��
��(2)�ЈA��һ�l�о������c(di��n)��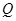 . ��(w��n)�Ƿ����һ��(g��)���c(di��n)
. ��(w��n)�Ƿ����һ��(g��)���c(di��n)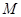 ������
������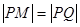 ��Ո(q��ng)�f(shu��)������.
��Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ABC�ăɂ�(g��)��c(di��n)����(bi��o)�քe��B(0��6)��C(0��-6)�����߅AB��AC��б�ʵij˷e��-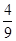 ������c(di��n)A��܉�E����.?
������c(di��n)A��܉�E����.?
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)�E�AC��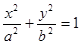
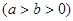 �^(gu��)�c(di��n)
�^(gu��)�c(di��n) , ���x����
, ���x����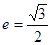 ��
��
(��)��E�A�õķ��̣�
(��)�^(gu��)�ҽ��c(di��n)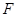 �Ą�(d��ng)ֱ�����E�A���c(di��n)
�Ą�(d��ng)ֱ�����E�A���c(di��n)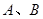 ���O(sh��)�E�A������c(di��n)��
���O(sh��)�E�A������c(di��n)��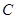 �B��
�B��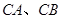 �ҽ���(d��ng)ֱ��
�ҽ���(d��ng)ֱ��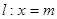 ��
��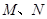 ������MN��ֱ���ĈA���^(gu��)�ҽ��c(di��n)F����
������MN��ֱ���ĈA���^(gu��)�ҽ��c(di��n)F����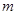 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com