Question

函數其中P，M為實數集R的兩個非空子集，又規定f(P)={y|y=f(x),x∈P}，f(M)={y|y=f(x),x∈M}.給出下列四個判斷：
①若P∩M=，則f(P)∩f(M)=；
②若P∩M≠，則f(P)∩f(M) ≠；
③若P∪M=R，則f(P)∪f(M)=R；
④若P∪M≠R，則f(P)∪f(M)≠R.
其中正確判斷有(     )
A  0個        B  1個       C  2個       D  4個

Answer 1

A

解析試題分析：函數的表達式知，可借助兩個函數y=x與y=-x圖象來研究，分析可得答案．
由題意知函數f（P）、f（M）的圖象如圖所示．

設

故①錯誤
同理可知當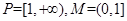
,②不正確．
設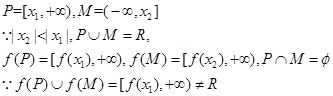

，故③錯誤．
④若則．這是不對的 若P={非負實數}，M={正實數}
則f（P）={非負實數}，f（M）={負實數}
則f（P）∪f（M）=R．故④錯,故選A
考點：本試題主要是考查了同學們對于與集合，函數相關的創新試題的分析，和解決問題能力的運用，是中檔題。
點評：考查對題設條件的理解與轉化能力，本題中題設條件頗多，審題費時，需仔細審題才能把握其脈絡，故研究時借用兩個函數的圖象，借助圖形的直觀來來幫助判斷命題的正誤，以形助數，是解決數學問題常用的一種思路。