
在直角坐標平面中,已知點![]() ,
, ![]() ,…
,…![]() , 其中n是正整數. 對平面上任一點
, 其中n是正整數. 對平面上任一點![]() , 記A1為A0關于點P1的對稱點, A2為A1關于點P2的對稱點, ┄, AN為AN-1關于點PN的對稱點.
, 記A1為A0關于點P1的對稱點, A2為A1關于點P2的對稱點, ┄, AN為AN-1關于點PN的對稱點.
(1)求向量![]() 的坐標;
的坐標;
(2)當點A0在曲線C上移動時, 點A2的軌跡是函數![]() 的圖象,其中
的圖象,其中![]() 是以3為周期的周期函數,且當x∈(0,3)時,
是以3為周期的周期函數,且當x∈(0,3)時,![]() =lgx.求以曲線C為圖象的函數在(1,4)上的解析式;
=lgx.求以曲線C為圖象的函數在(1,4)上的解析式;
(3)對任意偶數n,用n表示向量![]() 的坐標.
的坐標.
解:(1)法一: 設點A0(x,y), A1為A0關于點P1的對稱點,A1的坐標為(2-x,4-y),
A2為A1關于點P2的對稱點,A2的坐標為(2+x,4+y),
∴![]() =(2,4).
=(2,4).
法二:![]() =2
=2![]() , ∴
, ∴![]() =(2,4)
=(2,4)
(2) 法一∵![]() =(2,4),
=(2,4),
∴f(x)的圖象由曲線C向右平移2個單位,再向上平移4個單位得到.因此,
曲線C是函數y=g(x)的圖象,其中g(x)是以3為周期的周期函數,
且當x∈(-2,1]時,g(x)=lg(x+2)-4.于是, 當x∈(1,4)時, g(x)=lg(x-1)-4.
法二:設點A0(x,y), 則A2的坐標為(2+x,4+y)
∵點A2的軌跡是函數y=f(x)的圖象,于是當0<x+2≤3時,有y+4=lg(x+2),
即當-2< x≤1時, g(x)=y=lg(x+2)-4.
∴當x∈(1,4)時,g(x)=lg(x-1)-4.
(3)![]() =
=![]() , 由于
, 由于![]() ,得
,得
![]() =2(
=2(![]() ) =2((1,2)+(1,23)+…+(1,2n-1))
) =2((1,2)+(1,23)+…+(1,2n-1))
=2(![]() ,
,![]() ) = (n,
) = (n,![]() )
)


科目:高中數學 來源: 題型:
| A0A2 |
| A0An |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A0A2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| B0B10 |
查看答案和解析>>
科目:高中數學 來源:2008-2009學年上海市虹口區北郊高級中學高三(上)摸底數學試卷(解析版) 題型:解答題
 的坐標;
的坐標;查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省高三上學期期中考試數學文卷 題型:填空題
在直角坐標平面中,已知點 ,
, ,對平面上任意一點
,對平面上任意一點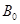 ,記
,記 為
為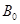 關于
關于 的對稱點,
的對稱點, 為
為 關于
關于 的對稱點,
的對稱點, 為
為 關于
關于 的對稱點,
的對稱點,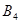 為
為 關于
關于 的對稱點,…,
的對稱點,…, 為
為 關于
關于 的對稱點,
的對稱點, 為
為 關于
關于 的對稱點,
的對稱點, 為
為 關于
關于 的對稱點
的對稱點 …。則
…。則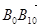 =
=
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com