
(2007
北京朝陽模擬)如下圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點(diǎn),D是點(diǎn)A在平面BCD內(nèi)的射影.(1)
求直線EF與直線BC所成角的大小;(2)
求點(diǎn)O到平面ACD的距離;(3)
求二面角A-BE-F的大小.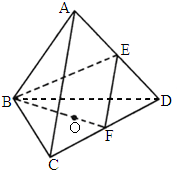
|
解析: (1)因?yàn)?/FONT>E、F分別是棱AD、CD的中點(diǎn).所以EF∥AC.所以∠ BCA是EF與BC所成角.∵正四面體 ABCD,∴△ABC為正三角形,所以∠ BCA=60°.即 EF與BC所成角的大小是60°.(2) 如圖,連結(jié)AO,AF,因?yàn)?/FONT>F是CD的中點(diǎn),且△ACD,△BCD均為正三角形,所以 BF⊥CD,AF⊥CD.因?yàn)?/FONT> 因?yàn)?/FONT>
因?yàn)?/FONT>ABCD是正四面體,且O是點(diǎn)A在面BCD內(nèi)的射影,所以點(diǎn)O必在正三角形BCD的中線BF上. 在面 ABF中,過O做OG⊥AF,垂足為G.所以OG⊥面ACD.即 OG的長為點(diǎn)O到面ACD的距離.因?yàn)檎拿骟w ABCD的棱長為1,在△ ABF中,容易求出 , ,
因?yàn)椤?/FONT>AOF∽△OGF,故由相似比易求出 所以點(diǎn) O到平面ACD的距離是 . .
(3) 設(shè)△ABD中,AB邊的中線交BE于H,連結(jié)CH,則由ABCD為正四面體知CH⊥面ABD.設(shè) HD的中點(diǎn)為K,則FK∥CH.所以FK⊥面ABD.在面 ABD內(nèi),過點(diǎn)K作KN∥AD,KN交BE于M,交AB于N,因?yàn)?/FONT>BE⊥AD,所以NM⊥BE. 連結(jié) FM,所以FM⊥BE.所以∠ NMF是所求二面角的平面角.
因?yàn)?/FONT> 所以  . .
所以  . .
所以所求二面角的大小為 
( 或者由正四面體的對稱性,可轉(zhuǎn)求二面角 的大小). 的大小). |



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:022
(2007
北京朝陽模擬)將正奇數(shù)劃分成下列組:(1),(3,5),(7,9,11),(13,15,17,19),…,則第n組各數(shù)的和是________,第n組的第一個(gè)數(shù)可以表示為_________.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:044
(2007
北京朝陽模擬)已知 (a≠0)是定義在R上的函數(shù),其圖象交x軸于A、B、C三點(diǎn).若點(diǎn)B的坐標(biāo)為(2,0),且f(x)在[-1,0]和[4,5]上有相同的單調(diào)性,在[0,2]和[4,5]上有相反的單調(diào)性.
(a≠0)是定義在R上的函數(shù),其圖象交x軸于A、B、C三點(diǎn).若點(diǎn)B的坐標(biāo)為(2,0),且f(x)在[-1,0]和[4,5]上有相同的單調(diào)性,在[0,2]和[4,5]上有相反的單調(diào)性.
(1)
求c的值;(2)
在函數(shù)f(x)的圖象上是否存在一點(diǎn)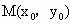 使得f(x)在點(diǎn)M處的切線斜率為3b?若存在,求出點(diǎn)M的坐標(biāo);若不存在,請說明理由;
使得f(x)在點(diǎn)M處的切線斜率為3b?若存在,求出點(diǎn)M的坐標(biāo);若不存在,請說明理由;
(3)
求|AC|的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:044
(2007
北京朝陽模擬)已知O為坐標(biāo)原點(diǎn),點(diǎn)E、F的坐標(biāo)分別為(-1,0)、(1,0),動(dòng)點(diǎn)A、M、N滿足 (m>1),
(m>1),
 .
.
(1)
求點(diǎn)M的軌跡W的方程;(2)
點(diǎn) 在軌跡W上,直線PF交軌跡W于點(diǎn)Q,且
在軌跡W上,直線PF交軌跡W于點(diǎn)Q,且 ,若1≤λ≤2,求實(shí)數(shù)m的范圍.
,若1≤λ≤2,求實(shí)數(shù)m的范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:044
(2007
北京朝陽模擬)已知向量 ,
, ,動(dòng)點(diǎn)M到定直線y=1的距離等于d,并且滿足
,動(dòng)點(diǎn)M到定直線y=1的距離等于d,并且滿足 ,其中O為坐標(biāo)原點(diǎn),k為參數(shù).
,其中O為坐標(biāo)原點(diǎn),k為參數(shù).
(1)
求動(dòng)點(diǎn)M的軌跡方程,并判斷曲線類型;(2)
如果動(dòng)點(diǎn)M的軌跡是一條圓錐曲線,其離心率e滿足 ,求實(shí)數(shù)k的取值范圍.
,求實(shí)數(shù)k的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:022
(2007
北京朝陽模擬)已知函數(shù) 且不等式
且不等式 的解集是(-∞,-2]∪[0,2],則實(shí)數(shù)a的值是_________.
的解集是(-∞,-2]∪[0,2],則實(shí)數(shù)a的值是_________.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com