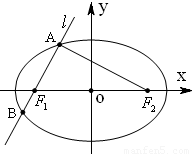
分析:(Ⅰ)因為在焦點三角形AF
1F
2中,
•=0,所以∠F
1AF
2=90°,又因為∠AF
1F
2=60°,所以
△AF1F2的三邊關系可以找到,根據三邊關系,可求出含a,c的齊次式,進而求出離心率.
(II)若
a=,b=1,則橢圓方程為兩個,可以是焦點在x軸上,也可焦點在y軸上,分別寫出方程,在與設出的直線l方程聯立,找到橫坐標之和與之積,用坐標表示
•,根據前面所求,得到含k的方程,再求出最值即可.
解答:解:(I)∵
•=0,∴AF
1⊥AF
2∵∠AF
1F
2=60°,∴F
1F
2=2AF
1,
AF2=AF1------(3分)
∴2a=AF
1+AF
2,2c=F
1F
2∴
離心率e===-1------(6分)
(II)∵
a=,b=1,∴c=1,點F
1(-1,0),F
2(1,0).
①若AB垂直于x軸,則
A(-1,),B(-1,-),
•=(0,)•(0,-)=-------(8分)
②若AB與x軸不垂直,設直線AB的斜率為k,
則直線AB的方程為 y=k(x+1)
由
消去y得:(2k
2+1)x
2+4k
2x+2k
2-2=0∵△=8k
2+8>0,∴方程有兩個不等的實數根.
設A(x
1,y
1),B(x
2,y
2).∴
x1+x2=-,
x1•x2=------(10分)
∴
=(x1+1,y1),=(x2+1,y2)•=(x1+1)(x2+1)+y1y2=(x1+1)(x2+1)+k2(x1+1)(x2+1)=(1+k
2)(x
1x
2+x
1+x
2+1)=
(1+k2)(-+1)=
-=---------(12分)
∵
k2≥0,2k2+1≥1, 0<≤1,∴
-1≤--<-∴
•∈[-1,-)------(14分)
綜合①、②可得:
•∈[-1,-].
所以當直線l垂直于x時,
•取得最大值
-;當直線l與x軸重合時,
•取得最小值-1------(15分)
點評:本題考查了利用焦點三角形三邊關系求橢圓方程,以及橢圓與向量相結合求最值,注意解題過程中,設而不求思想的應用.

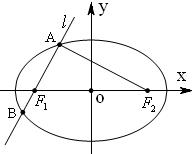 如圖已知,橢圓
如圖已知,橢圓

 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案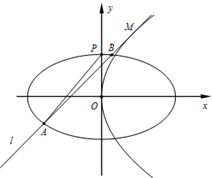 如圖,已知:橢圓
如圖,已知:橢圓 的左、右焦點分別為
的左、右焦點分別為 、
、 ,過
,過 的直線
的直線 與橢圓相交于A、B兩點。
與橢圓相交于A、B兩點。 ,且
,且 ,求橢圓的離心率;
,求橢圓的離心率; 求
求 的最大值和最小值。
的最大值和最小值。
 的左、右焦點分別為F1、F2,過F1的直線l與橢圓相交于A、B兩點.
的左、右焦點分別為F1、F2,過F1的直線l與橢圓相交于A、B兩點.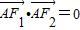 ,求橢圓的離心率;
,求橢圓的離心率;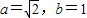 ,求
,求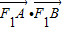 的最大值和最小值.
的最大值和最小值.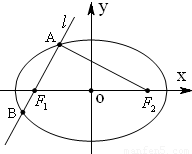
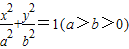 的左、右焦點分別為F1、F2,過F1的直線l與橢圓相交于A、B兩點.
的左、右焦點分別為F1、F2,過F1的直線l與橢圓相交于A、B兩點.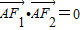 ,求橢圓的離心率;
,求橢圓的離心率;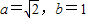 ,求
,求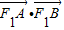 的最大值和最小值.
的最大值和最小值.