
有甲、乙兩個班級進行數學考試,按照大于或等于85分為優秀,85分以下為非優秀統計成績后,得到如下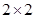 聯表:
聯表:
| | 優秀 | 非優秀 | 合計 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合計 | | | 200 |
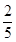
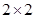 聯表;
聯表;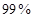 的把握認為“成績與班級有關系”
的把握認為“成績與班級有關系” ,若每次抽取得結果是相互獨立的,求
,若每次抽取得結果是相互獨立的,求 的分布列,期望
的分布列,期望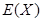 和方差
和方差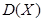

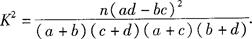
(1)
(2) 優秀 非優秀 合計 甲班 30 70 100 乙班 50 50 100 合計 80 120 200 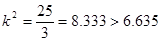 ,有
,有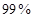 的把握
的把握
(3)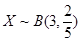 ,
,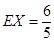 ,
,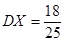
解析試題分析:(1)根據題意,由于全部200人中隨機抽取1人為優秀的概率為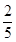 ,那么可知優秀的人數為80,那么可知不優秀的人數為120,那么可知得到列聯表為:
,那么可知優秀的人數為80,那么可知不優秀的人數為120,那么可知得到列聯表為:
(2)根據a=30,b=70,c=50,d=120,結合公式 優秀 非優秀 合計 甲班 30 70 100 乙班 50 50 100 合計 80 120 200 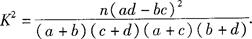 ,可知
,可知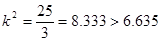 ,有
,有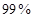 的把握認為“成績與班級有關系”
的把握認為“成績與班級有關系”
(3)由于全部200人中有放回抽取3次,每次抽取一人,記被抽取的3人中優秀的人數為 ,那么可知
,那么可知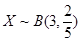 ,
,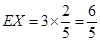 ,
,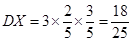 ,。
,。
考點:列聯表和獨立性檢驗
點評:主要是考查了獨立性檢驗的思想的運用,以及二項分布的運用,屬于中檔題。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
2012年第三季度,國家電網決定對城鎮居民民用電計費標準做出調整,并根據用電情況將居民分為三類: 第一類的用電區間在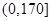 ,第二類在
,第二類在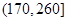 ,第三類在
,第三類在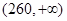 (單位:千瓦時). 某小區共有1000戶居民,現對他們的用電情況進行調查,得到頻率分布直方圖如圖所示.
(單位:千瓦時). 某小區共有1000戶居民,現對他們的用電情況進行調查,得到頻率分布直方圖如圖所示.
⑴ 求該小區居民用電量的中位數與平均數;
⑵ 本月份該小區沒有第三類的用電戶出現,為鼓勵居民節約用電,供電部門決定:對第一類每戶獎勵20元錢,第二類每戶獎勵5元錢,求每戶居民獲得獎勵的平均值;
⑶ 利用分層抽樣的方法從該小區內選出5戶居民代表,若從該5戶居民代表中任選兩戶居民,求這兩戶居民用電資費屬于不同類型的概率. 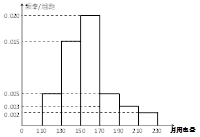
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一臺機器使用的時間較長,但還可以使用,它按不同的轉速生產出來的某機械零件有一些會有缺點,每小時生產有缺點零件的多少,隨機器的運轉的速度而變化,下表為抽樣試驗的結果:
| 轉速x(轉/秒) | 16 | 14 | 12 | 8 |
| 每小時生產有缺點的零件數y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學號召本校學生在本學期參加市創辦衛生城的相關活動,學校團委對該校學生是否關心創衛活動用簡單抽樣方法調查了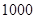 位學生(關心與不關心的各一半),
位學生(關心與不關心的各一半),
結果用二維等高條形圖表示,如圖.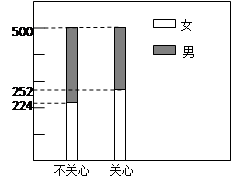
(1)完成列聯表,并判斷能否有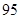 ℅的把握認為是否關心創衛活動與性別有關?
℅的把握認為是否關心創衛活動與性別有關?
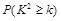 | 0.10 | 0.05 | 0.01 |
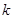 | 2.706 | 3.841 | 6.635 |
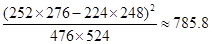
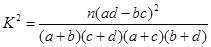 ;
;| | 女 | 男 | 合計 |
| 關心 | | | 500 |
| 不關心 | | | 500 |
| 合計 | | 524 | 1000 |
| 參加活動次數 | 1 | 2 | 3 |
| 人數 | 10 | 50 | 40 |
 表示這兩人參加活動次數之差的絕對值,求隨機變量
表示這兩人參加活動次數之差的絕對值,求隨機變量 的分布列及數學期望
的分布列及數學期望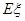 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為調查某地區大學生是否愛好某項體育運動,用簡單隨機抽樣方法從該地區的大學里調查了500位大學生,結果如下:
| | 男 | 女 |
| 愛好 | 40 | 30 |
| 不愛好 | 160 | 270 |
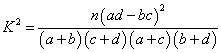
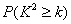 | 0.050 | 0.010 | 0.001 |
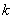 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(t)與相應的生產能耗y(t標準煤)的幾組對照數據.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 ;
;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校的研究性學習小組為了研究高中學生的身體發育狀況,在該校隨機抽出120名17至18周歲的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人數各占一半
(1)根據以上數據建立一個 列聯表:
| | 偏重 | 不偏重 | 合計 |
| 偏高 | | | |
| 不偏高 | | | |
| 合計 | | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校從參加考試的學生中抽出60名學生,將其成績(均為整數)分成六組[40,50),[50,60) ...[90,100]后畫出如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
(1)求成績落在[70,80)上的頻率,并補全這個頻率分布直方圖;
(2)估計這次考試的及格率(60分及以上為及格)和平均分;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某大學體育學院在2012年新招的大一學生中,隨機抽取了 40名男生,他們的身高(單位:cm)情況共分成五組:第1組[175,180),第 2 組[180,185),第 3 組 [185,190),第 4 組[190,195),第 5 組[195,200) .得到的頻率分布直方圖(局部)如圖所示,同時規定身高在185cm以上(含185cm)的學生成為組建該校籃球隊的“預備生”.
(I)求第四組的頻率并補布直方圖;
(II)如果用分層抽樣的方法從“預備生”和“非預備生”中選出5人,再從這5人中隨機選2人,那么至少有1人是“預備生”的概率是多少?
(III)若該校決定在第4,5組中隨機抽取2名學生接受技能測試,第5組中有ζ名學生接受測試,試求ζ的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com