
(2)已知tanα=3,求sinα和cosα的值;
(3)已知sinα=m(|m|≤1),求cosα和tanα的值.
思路分析:(1)直接利用同角三角函數(shù)的基本關(guān)系式和角的范圍求值;(2)應(yīng)注意角的終邊位置有兩種即第一、三象限,所以結(jié)果有兩種;(3)則需要分類(lèi)討論.
解:(1)因?yàn)閟in2α+cos2α=1,
所以cos2α=1-sin2α=1-(![]() )2=
)2=![]() .
.
又因?yàn)?I >α是第二象限角,所以cosα<0,
于是![]() .
.
從而![]() .
.
(2)因?yàn)閟in2α+cos2α=1,所以sin2α=1-cos2α.
又因?yàn)?SUB>![]() ,
,
所以![]() .
.
于是![]() ,
,![]() .
.
因?yàn)閠anα=3>0,所以角α是第一或第三象限的角.
如果α是第一象限角,那么
![]() ,sinα=tanαcosα=
,sinα=tanαcosα=![]() .
.
如果α是第三象限角,那么
![]() ,sinα=tanαcosα=
,sinα=tanαcosα=![]() .
.
(3)①若m=±1,由sin2α+cos2α=1,得cos2α=1-sin2α=1-(±1)2=0,
所以cosα=0,tanα不存在.
②若m=0,則角α的終邊在x軸上,由sin2α+cos2α=1,得cos2α=1-sin2α=1-02=1.
當(dāng)角α的終邊在x軸正半軸上時(shí),cosα=1,tanα=0;
當(dāng)角α的終邊在x軸負(fù)半軸上時(shí),cosα=-1,tanα=0.
③若0<|m|<1時(shí),
當(dāng)角α的終邊在第一象限或第四象限時(shí),由sin2α+cos2α=1,得![]() ,;
,;![]()
當(dāng)角α的終邊在第二象限或第三象限時(shí),由sin2α+cos2α=1,得![]() ,
,![]() .
.
綜上,可知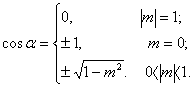
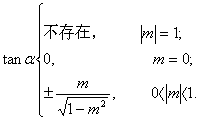
深化升華 利用同角的三角函數(shù)基本關(guān)系式,在已知一個(gè)三角函數(shù)值而求其他三角函數(shù)值時(shí),應(yīng)首先根據(jù)所給的三角函數(shù)值和已知條件判斷角的終邊位置,如果沒(méi)法判斷的話(huà)應(yīng)注意分類(lèi)討論.而在具體求解時(shí)應(yīng)首先利用平方關(guān)系,再利用其他關(guān)系.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 3 | 5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
| 1+tanα |
| 1-tanα |
| 2sinα-3cosα |
| 4sinα-9cosα |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| 17 |
| 13 |
| 2sinα-cosα |
| sinα+3cosα |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| sin(π-α)+5cos(2π-α) | ||
2sin(
|
tan(π-α)cos(2π-α)sin(-α+
| ||
| cos(-α-π)sin(-π-α) |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com