
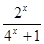 .
.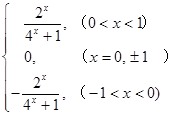 . (2)用定義或導數法均可證明;(3)λ<
. (2)用定義或導數法均可證明;(3)λ<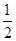
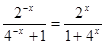 .
. 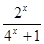 . 2分
. 2分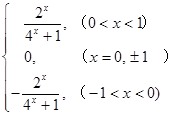 . 6分
. 6分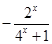 ,∵
,∵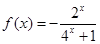 ,∴
,∴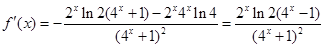 ,又-1<x<0,∴
,又-1<x<0,∴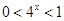 ,∴
,∴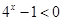 ,∴
,∴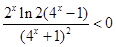 ,∴f (x)在(—1, 0)上時減函數 10分
,∴f (x)在(—1, 0)上時減函數 10分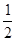 < f(x)= -
< f(x)= -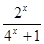 < -
< -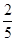 ;
;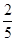 < f(x)=
< f(x)=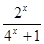 <
<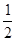 ;
;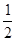 , -
, -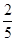 )∪{0}∪(
)∪{0}∪(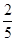 ,
, 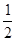 ). 14分
). 14分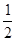 , -
, -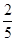 )∪{0}∪(
)∪{0}∪(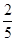 ,
, 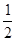 ) 15分
) 15分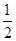 時,不等式f(x)>λ在R上有解. 16分
時,不等式f(x)>λ在R上有解. 16分 的奇偶性把
的奇偶性把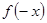 寫成
寫成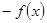 或
或 ,從而求出
,從而求出 .
.

科目:高中數學 來源:不詳 題型:填空題
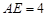 米,
米,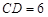 米. 為了合理利用這塊鋼板,將在五邊形
米. 為了合理利用這塊鋼板,將在五邊形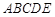 內截取一個矩形塊
內截取一個矩形塊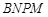 ,使點
,使點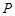 在邊
在邊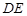 上. 則矩形
上. 則矩形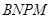 面積的最大值為____ 平方米 .
面積的最大值為____ 平方米 . 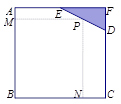
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
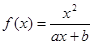 (a,b為常數)且方程f(x)-x+12=0有兩個實根為x1="3," x2=4.
(a,b為常數)且方程f(x)-x+12=0有兩個實根為x1="3," x2=4.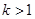 ,解關于x的不等式;
,解關于x的不等式;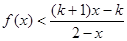 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 、縱邊
、縱邊 設計為多少米時,才能使圍成的網箱中篩網的總長度最小?
設計為多少米時,才能使圍成的網箱中篩網的總長度最小?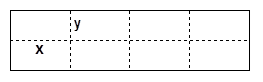
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
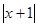 ,g(x)=2|x|+a.
,g(x)=2|x|+a.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
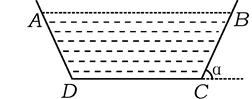
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com