
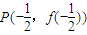 處的切線與y軸交于點Qn(0,yn).
處的切線與y軸交于點Qn(0,yn).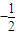 處的導函數值,再結合導數的幾何意義即可求出切線的斜率進而求出切線方程最后得到與y軸交點坐標.從而問題解決.
處的導函數值,再結合導數的幾何意義即可求出切線的斜率進而求出切線方程最后得到與y軸交點坐標.從而問題解決.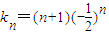 ,(2分)
,(2分)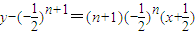 ,(3分)
,(3分)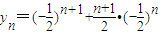 ,
,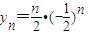 .(4分)
.(4分) ①
①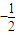 得:
得: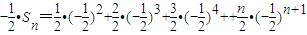 ②
②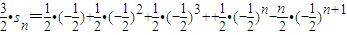 (6分)
(6分)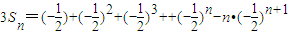
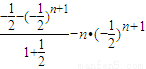
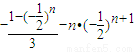
 (8分)
(8分)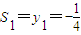 ,S2=y1+y2=0,
,S2=y1+y2=0,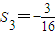 ,
,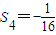
 ;(11分)
;(11分)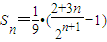 ,
,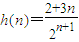 ,則
,則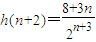 .
.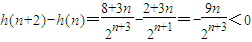 ,
,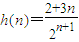 的最大值為h(2)=1,即Sn的最大值為S2=0.(14分)
的最大值為h(2)=1,即Sn的最大值為S2=0.(14分)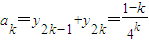 ,顯然a1=0,k>1,ak<0,
,顯然a1=0,k>1,ak<0,

 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2011年廣東省東莞高級中學高考數學二模試卷(文科)(解析版) 題型:解答題
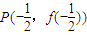 處的切線與y軸交于點Qn(0,yn).
處的切線與y軸交于點Qn(0,yn).查看答案和解析>>
科目:高中數學 來源:2011年廣東省東莞高級中學高考數學二模試卷(理科)(解析版) 題型:解答題
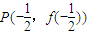 處的切線與y軸交于點Qn(0,yn).
處的切線與y軸交于點Qn(0,yn).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com