
設f(x)是定義在[0,1]上的函數,若存在x*∈(0,1),使得f(x)在[0, x*]上單調遞增,在[x*,1]上單調遞減,則稱f(x)為[0,1]上的單峰函數,x*為峰點,包含峰點的區間為含峰區間.對任意的[0,l]上的單峰函數f(x),下面研究縮短其含峰區間長度的方法.
(1)證明:對任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),則(0,x2)為含峰區間;若f(x1)≤f(x2),則(x*,1)為含峰區間;
(2)對給定的r(0<r<0.5=,證明:存在x1,x2∈(0,1),滿足x2-x1≥2r,使得由
(I)所確定的含峰區間的長度不大于0.5+r;
(3)選取x1,x2∈(0,1),x1<x2,由(I)可確定含峰區間為(0,x2)或(x1,1),在所得的含峰區間內選取x3,由x3與x1或x3與x2類似地可確定一個新的含峰區間.在第一次確定的含峰區間為(0,x2)的情況下,試確定x1,x2,x3的值,滿足兩兩之差的絕對值不小于0.02,且使得新的含峰區間的長度縮短到0.34.(區間長度等于區間的右端點與左端點之差)
(1)證明:設x*為f(x) 的峰點,則由單峰函數定義可知,f(x)在[0, x*]上單調遞增,在[x*,1]上單調遞減.
當f(x1)≥f(x2)時,假設x*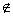 (0,x2),則x1<x2<x*,從而f(x*)≥f(x2) >f(x1),這與f(x1)≥f(x2)矛盾,所以x*∈(0,x2),即(0,x2)是含峰區間.
(0,x2),則x1<x2<x*,從而f(x*)≥f(x2) >f(x1),這與f(x1)≥f(x2)矛盾,所以x*∈(0,x2),即(0,x2)是含峰區間.
當f(x1)≤f(x2)時,假設x*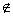 ( x2,1),則x*<≤x1<x2,從而f(x*)≥f(x1)>f(x2),
( x2,1),則x*<≤x1<x2,從而f(x*)≥f(x1)>f(x2),
這與f(x1)≤f(x2)矛盾,所以x*∈(x1,1),即(x1,1)是含峰區間.…………4分
(2)證明:由(I)的結論可知:
當f(x1)≥f(x2)時,含峰區間的長度為l1=x2;當f(x1)≤f(x2)時,含峰區間的長度為l2=1-x1;
對于上述兩種情況,由題意, 得
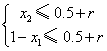 ① …………………………6分
① …………………………6分
由①得1+x2-x1≤1+2r,即x1-x1≤2r.
又因為x2-x1≥2r,所以x2-x1=2r, ②
將②代入①得x1≤0.5-r, x2≥0.5-r, ③ …………………………8分
由①和③解得 x1=0.5-r, x2=0.5+r.
所以這時含峰區間的長度l1=l1=0.5+r,即存在x1,x2使得所確定的含峰區間的長度不大于0.5+r。…………………………10分
(3)解:對先選擇的x1;x2,x1<x2,由(II)可知x1+x2=l, ④
在第一次確定的含峰區間為(0, x2)的情況下,x3的取值應滿足x3+x1=x2, ⑤
由④與⑤可得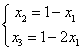 ,當x1>x3時,含峰區間的長度為x1。
,當x1>x3時,含峰區間的長度為x1。
由條件x1-x3≥0.02,得x1-(1-2x1)≥0.02,從而x1≥0.34。
因此,為了將含峰區間的長度縮短到0.34,只要取x1=0.34,x2=0.66,x3=0.32.
………………14分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 | 4 |
| 3 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com