
(1)設P、Q兩點坐標分別為(x1,y1)、(x2,y2),證明y1·y2=-p2;
(2)求拋物線的方程;
(3)試判斷在拋物線上是否存在一點,使該點與點M關于PN所在的直線對稱?若存在,請求出此點的坐標;若不存在,請說明理由.
思路分析:本題是一道與物理中的光學知識相結合的綜合性題目.
證明:由拋物線的光學性質及題意,知光線PQ必過拋物線的焦點F(![]() ,0),設直線PQ的方程為y=k(
,0),設直線PQ的方程為y=k(![]() ), ①
), ①
由①式,得x=![]() .
.
將其代入拋物線方程y2=2px中,整理得y2-![]() -p2=0.由韋達定理,y1y2=-p2.
-p2=0.由韋達定理,y1y2=-p2.
當直線PQ的斜率角為90°時,將x=![]() 代入拋物線方程,得y=±p,同樣得到y1·y2=-p2.
代入拋物線方程,得y=±p,同樣得到y1·y2=-p2.
(2)解:因為光線QN經直線l反射后又射向M點,所以直線MN與直線QN關于直線l對稱.設點M(![]() ,4)關于l的對稱點為M′(x′,y′),
,4)關于l的對稱點為M′(x′,y′),
則 解得
解得
直線QN的方程為y=-1,Q點的縱坐標y2=-1.
由題設P點的縱坐標y1=4,且由(1)知:y1·y2=-p2,則4·(-1)=-p2,得p=2.
故所求拋物線方程為y2=4x.
(3)解:將y=4代入y2=4x,得x=4.故P點坐標為(4,4).將y=-1代入直線l的方程為2x-4y-17=0.得x=![]() .故N點坐標為(
.故N點坐標為(![]() ,-1).由P、N兩點坐標得直線PN的方程為2x+y-12=0.
,-1).由P、N兩點坐標得直線PN的方程為2x+y-12=0.
設M點關于直線NP的對稱點為M1(x1,y1),
則
解得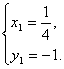
又M1(![]() ,-1)的坐標是拋物線方程y2=4x的解,
,-1)的坐標是拋物線方程y2=4x的解,
故拋物線上存在一點(![]() ,-1)與點M關于直線PN對稱.
,-1)與點M關于直線PN對稱.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
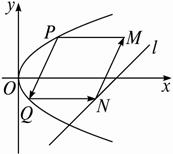
 拋物線有光學性質:由其焦點射出的光線經拋物線反象后,沿平行于拋物線對稱軸的肖向射出,反之亦然.如圖所示,今有拋物線C,其頂點是坐標原點,對稱輔為x軸.開口向右.一光源在點M處,由其發出一條平行于x軸的光線射向拋物線C卜的點P(4.4),經拋物線C反射后,反射光線經過焦點F后射向拋物線C上的點Q,再經拋物線C反射后又沿平行于X軸的方向射出,途中經直線l:2x-4y-17=0上點N反射后又射回點M.
拋物線有光學性質:由其焦點射出的光線經拋物線反象后,沿平行于拋物線對稱軸的肖向射出,反之亦然.如圖所示,今有拋物線C,其頂點是坐標原點,對稱輔為x軸.開口向右.一光源在點M處,由其發出一條平行于x軸的光線射向拋物線C卜的點P(4.4),經拋物線C反射后,反射光線經過焦點F后射向拋物線C上的點Q,再經拋物線C反射后又沿平行于X軸的方向射出,途中經直線l:2x-4y-17=0上點N反射后又射回點M.查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西穩派名校學術聯盟高三12月調研文科數學試卷(解析版) 題型:選擇題
拋物線有光學性質:由其焦點射出的光線經拋物線折射后,沿平行于拋物線對稱軸的方向射出。現已知拋物線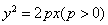 的焦點為F,過拋物線上點
的焦點為F,過拋物線上點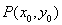 的切線為
的切線為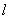 ,過P點作平行于x軸的直線m,過焦點F作平行于
,過P點作平行于x軸的直線m,過焦點F作平行于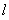 的直線交m于M,則
的直線交m于M,則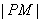 的長為( )
的長為( )
A. 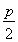 B.
B. 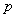 C.
C. 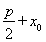 D.
D. 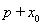
查看答案和解析>>
科目:高中數學 來源: 題型:

(1)設P、Q兩點的坐標分別為(x1,y1),(x2,y2),證明:y1y2=-p2;
(2)求拋物線的方程;
(3)試判斷在拋物線上是否存在一點,使該點與點M關于PN所在的直線對稱?若存在,請求出此點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2008-2009學年廣東省佛山一中高二(上)期末數學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com