
已知 是定義域為R的奇函數,
是定義域為R的奇函數,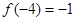 ,
, 的導函數
的導函數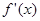 的圖象如圖所示。若兩正數
的圖象如圖所示。若兩正數 滿足
滿足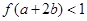 ,則
,則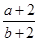 的取值范圍是
的取值范圍是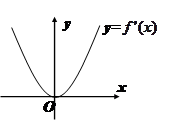
A.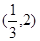 | B.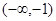 | C. | D.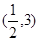 |
D
解析試題分析:先由導函數f′(x)是過原點的二次函數入手,再結合f(x)是定義域為R的奇函數求出f(x);然后根據a、b的約束條件畫出可行域,最后利用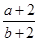 的幾何意義解決問題.解:由f(x)的導函數f’(x)的圖象,設f’(x)=mx2,則f(x)=
的幾何意義解決問題.解:由f(x)的導函數f’(x)的圖象,設f’(x)=mx2,則f(x)=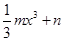 ,∵f(x)是定義域為R的奇函數,∴f(0)=0,即n=0,又f(-4)=
,∵f(x)是定義域為R的奇函數,∴f(0)=0,即n=0,又f(-4)=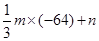 =-1,∴f(x)=
=-1,∴f(x)=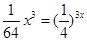
且f(a+2b)=( ,又a>0,b>0,則畫出點(b,a)的可行域如下圖所示
,又a>0,b>0,則畫出點(b,a)的可行域如下圖所示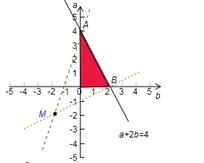
而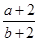 可視為可行域內的點(b,a)與點M(-2,-2)連線的斜率.又因為kAM=3,kBM=
可視為可行域內的點(b,a)與點M(-2,-2)連線的斜率.又因為kAM=3,kBM=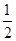
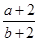 的取值范圍是
的取值范圍是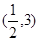 ,選D.
,選D.
考點:斜率的幾何意義
點評:數形結合是數學的基本思想方法:遇到二元一次不定式組要考慮線性規劃,遇到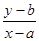 的代數式要考慮點(x,y)與點(a,b)連線的斜率.這都是由數到形的轉化策略
的代數式要考慮點(x,y)與點(a,b)連線的斜率.這都是由數到形的轉化策略


科目:高中數學 來源: 題型:單選題
.設三次函數 的導函數為
的導函數為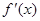 ,函數
,函數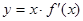 的圖象的一部分如圖所示,則正確的是
的圖象的一部分如圖所示,則正確的是 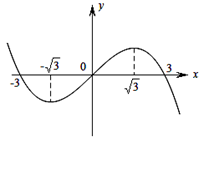
A. 的極大值為 的極大值為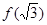 ,極小值為 ,極小值為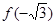 |
B. 的極大值為 的極大值為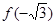 ,極小值為 ,極小值為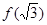 |
C. 的極大值為 的極大值為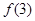 ,極小值為 ,極小值為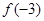 |
D. 的極大值為 的極大值為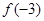 ,極小值為 ,極小值為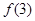 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com