
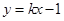 與拋物線C:
與拋物線C: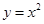 ,相交于兩點
,相交于兩點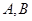 ,設點
,設點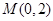 ,
,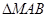 的面積為
的面積為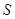 .
.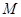 連線距離為
連線距離為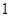 的點至多存在一個,求
的點至多存在一個,求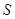 的范圍。
的范圍。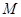 連線的距離為
連線的距離為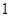 的點有兩個,分別記為
的點有兩個,分別記為 ,且滿足
,且滿足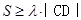 恒成立,求正數
恒成立,求正數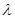 的范圍.
的范圍. 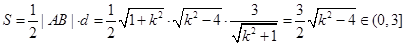 ;
;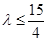 。
。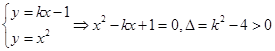 ,即
,即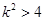 … (1)
… (1)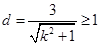 ,
,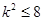 …(2)
…(2)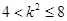
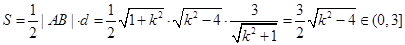 …………………7分
…………………7分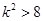 ,且
,且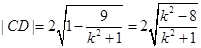
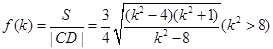 ,
, 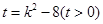 ,
,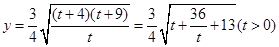 ,當且僅當
,當且僅當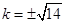 取到最小值是
取到最小值是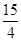
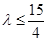 …………………………14分
…………………………14分

科目:高中數學 來源:不詳 題型:解答題
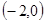 、B
、B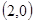 、C
、C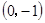 三點,過坐標原點O的直線
三點,過坐標原點O的直線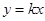 與拋物線交于M、N兩點.分別過點C、D
與拋物線交于M、N兩點.分別過點C、D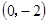 作平行于
作平行于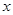 軸的直線
軸的直線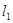 、
、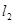 .(1)求拋物線對應的二次函數的解析式;(2)求證:以ON為直徑的圓與直線
.(1)求拋物線對應的二次函數的解析式;(2)求證:以ON為直徑的圓與直線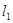 相切;(3)求線段MN的長(用
相切;(3)求線段MN的長(用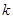 表示),并證明M、N兩點到直線
表示),并證明M、N兩點到直線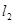 的距離之和等于線段MN的長.
的距離之和等于線段MN的長.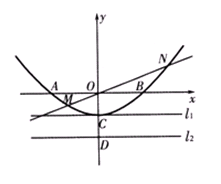
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
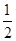 )到拋物線C:y
)到拋物線C:y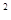 =2px(P>0)的準線的距離為
=2px(P>0)的準線的距離為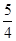 .點M(t,1)是C上的定點,A,B是C上的兩動點,且線段AB被直線OM平分.
.點M(t,1)是C上的定點,A,B是C上的兩動點,且線段AB被直線OM平分.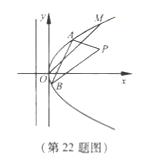
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com