
(07年湖南卷文)(14分)
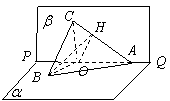
如圖,已知直二面角![]() ,直線CA和平面
,直線CA和平面![]() 所成的角為
所成的角為![]() .
.
(Ⅰ)證明![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.

解析:(I)在平面![]() 內(nèi)過點(diǎn)
內(nèi)過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,連結(jié)
,連結(jié)![]() .
.
因?yàn)?IMG height=21 src='http://thumb.zyjl.cn/pic1/img/20090326/20090326142301006.gif' width=47>,![]() ,所以
,所以![]() ,又因?yàn)?IMG height=19 src='http://thumb.zyjl.cn/pic1/img/20090326/20090326142301009.gif' width=61>,所以
,又因?yàn)?IMG height=19 src='http://thumb.zyjl.cn/pic1/img/20090326/20090326142301009.gif' width=61>,所以![]() .
.
而![]() ,所以
,所以![]() ,
,![]() .從而
.從而![]() .又
.又![]() ,
,
所以![]() 平面
平面![]() .因?yàn)?IMG height=19 src='http://thumb.zyjl.cn/pic1/img/20090326/20090326142312017.gif' width=41>平面
.因?yàn)?IMG height=19 src='http://thumb.zyjl.cn/pic1/img/20090326/20090326142312017.gif' width=41>平面![]() ,故
,故![]() .
.
(II)解法一:由(I)知,![]() ,又
,又![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,連結(jié)
,連結(jié)![]() ,由三垂線定理知,
,由三垂線定理知,![]() .
.
故![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由(I)知,![]() ,所以
,所以![]() 是
是![]() 和平面
和平面![]() 所成的角,則
所成的角,則![]() ,
,
不妨設(shè)![]() ,則
,則![]() ,
,![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
于是在![]() 中,
中, .
.
故二面角![]() 的大小為
的大小為![]() .
.
解法二:由(I)知,![]() ,
,![]() ,
,![]() ,故可以
,故可以![]() 為原點(diǎn),分別以直線
為原點(diǎn),分別以直線![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標(biāo)系(如圖).
軸建立空間直角坐標(biāo)系(如圖).

因?yàn)?IMG height=19 src='http://thumb.zyjl.cn/pic1/img/20090326/20090326142301008.gif' width=57>,所以![]() 是
是![]() 和平面
和平面![]() 所成的角,則
所成的角,則![]() .
.
不妨設(shè)![]() ,則
,則![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
所以![]() .
.
則相關(guān)各點(diǎn)的坐標(biāo)分別是
![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
設(shè)![]()
![]() 是平面
是平面![]() 的一個法向量,由
的一個法向量,由 得
得
取![]() ,得
,得![]() .
.
易知![]() 是平面
是平面![]() 的一個法向量.
的一個法向量.
設(shè)二面角![]() 的平面角為
的平面角為![]() ,由圖可知,
,由圖可知,![]() .
.
所以 .
.
故二面角![]() 的大小為
的大小為![]() .
.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(07年湖南卷文)如圖1,在正四棱柱 ![]() 中,E、F分別是
中,E、F分別是![]() 的中點(diǎn),則以下結(jié)論中不成立的是
的中點(diǎn),則以下結(jié)論中不成立的是
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(07年湖南卷文)根據(jù)某水文觀測點(diǎn)的歷史統(tǒng)計數(shù)據(jù),得到某條河流水位的頻率分布直方圖(如圖2),從圖中可以看出,該水文觀測點(diǎn)平均至少一百年才遇到一次的洪水的最低水位是
A.48米 B. 49米 C. 50米 D. 51米

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com