

(1)求雙曲線S的方程;
(2)當k=1時,在雙曲線S的上支上求點B,使其與直線l的距離為![]() ;
;
(3)當0≤k<1時,若雙曲線S的上支上有且只有一個點B到直線l的距離為![]() ,求斜率k的值及相應的點B的坐標.
,求斜率k的值及相應的點B的坐標.
思路解析:本題是直線方程、點到直線的距離、圓、雙曲線等知識的綜合運用.(1)、(2)按條件求解不難.(3)可用數形結合,作一條與l平行且與l相距為![]() 的直線l′,使l′與雙曲線S的上支相切,切點即為所求.
的直線l′,使l′與雙曲線S的上支相切,切點即為所求.
解:(1)由已知得雙曲線的漸近線為y=±x,因而S為等軸雙曲線,頂點A′與A(![]() ,0)關于直線y=x對稱.∴A′(0,
,0)關于直線y=x對稱.∴A′(0,![]() ),∴所求雙曲線S的方程為y2-x2=2.
),∴所求雙曲線S的方程為y2-x2=2.
(2)若B(x,![]() )是雙曲線S的上支上到l:y=x-
)是雙曲線S的上支上到l:y=x-![]() 的距離為
的距離為![]() 的點,則
的點,則![]() =
=![]() ,解得x=
,解得x=![]() ,y=2,∴點B的坐標為(
,y=2,∴點B的坐標為(![]() ,2).
,2).
(3)當0≤k<1時,雙曲線S的上支在直線l的上方,∴點B在直線l的上方,設直線l′與l:y=k(x-![]() )平行且距離為
)平行且距離為![]() ,直線l′在l的上方,雙曲線S的上支上有且只有一個點B到直線l的距離為
,直線l′在l的上方,雙曲線S的上支上有且只有一個點B到直線l的距離為![]() ,等價于直線l′與雙曲線S的上支有且只有一個公共點.設l′的方程為y=kx+m,由于l上的點A到l′的距離為
,等價于直線l′與雙曲線S的上支有且只有一個公共點.設l′的方程為y=kx+m,由于l上的點A到l′的距離為![]() ,可知
,可知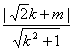 =
=![]() ,解得m=
,解得m=![]() (±
(±![]() -k).∵直線l′在直線l的上方,∴m=
-k).∵直線l′在直線l的上方,∴m=![]() (
(![]() -k).由方程y2-x2=2及y=kx+m消去y,得(k2-1)x2+2mkx+m2-2=0.
-k).由方程y2-x2=2及y=kx+m消去y,得(k2-1)x2+2mkx+m2-2=0.
∵k2≠1,∴Δ=4(m2-2+2k2)=8k(3k-2![]() ).
).
令Δ=0,∵0≤k<1,解得k=0或k=![]()
![]() .
.
當k=0時,m=![]() ,解得點B的坐標為(0,
,解得點B的坐標為(0, ![]() );
);
當k=![]()
![]() 時,m=
時,m=![]() ,解得點B的坐標為(2
,解得點B的坐標為(2![]() ,
,![]() ).
).


科目:高中數學 來源: 題型:
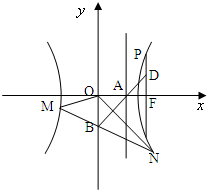 (2008•湖北模擬)如圖,已知雙曲線
(2008•湖北模擬)如圖,已知雙曲線| x2 |
| a2 |
| y2 |
| b2 |
| OD |
| OF |
| OP |
| AB |
| AD |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:044
已知雙曲線S的兩條漸近線過坐標原點,且與以點A(![]() ,0)為圓心,1為半徑的圓相切,雙曲線S的一個頂點A′與點A關于直線y=x對稱.設直線l過點A,斜率為k.
,0)為圓心,1為半徑的圓相切,雙曲線S的一個頂點A′與點A關于直線y=x對稱.設直線l過點A,斜率為k.
(1)求雙曲線S的方程;
(2)當k=1時,在雙曲線S的上支上求點B,使其與直線l的距離為![]() ;
;
(3)當0≤k<1時,若雙曲線S的上支上有且只有一個點B到直線l的距離為![]() ,求斜率k的值及相應的點B的坐標,如圖.
,求斜率k的值及相應的點B的坐標,如圖.
查看答案和解析>>
科目:高中數學 來源: 題型:

(1)求雙曲線S的方程;
(2)當k=1時,在雙曲線S的上支上,求點B,使其與直線l的距離為![]() .
.
查看答案和解析>>
科目:高中數學 來源:2007-2008學年湖北省宜昌一中、枝江一中、當陽一中三校聯合體高三2月聯考數學試卷(文科)(解析版) 題型:解答題
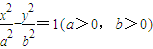 ,其右準線交x軸于點A,雙曲線虛軸的下端點為B.過雙曲線的右焦點F(c,0)作垂直于x軸的直線交雙曲線于點P,若點D滿足
,其右準線交x軸于點A,雙曲線虛軸的下端點為B.過雙曲線的右焦點F(c,0)作垂直于x軸的直線交雙曲線于點P,若點D滿足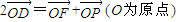 ,
,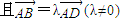 .
.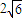 ,求l的方程.
,求l的方程.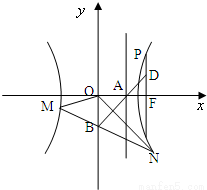
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com