
設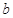 和
和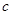 分別是先后拋擲一枚骰子得到的點數,用隨機變量
分別是先后拋擲一枚骰子得到的點數,用隨機變量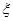 表示方程
表示方程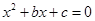 實根的個數(重根按一個計).
實根的個數(重根按一個計).
(1)求方程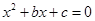 有實根的概率;
有實根的概率;
(2)求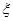 的分布列和數學期望;
的分布列和數學期望;
(3)求在先后兩次出現的點數中有5的條件下,方程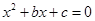 有實根的概率.
有實根的概率.
 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:解答題
高一(1)班參加校生物競賽學生成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如下,據此解答如下問題: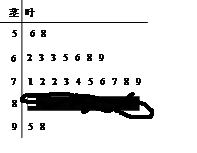
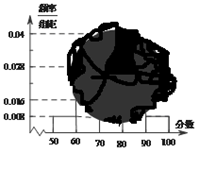
(1)求高一(1)班參加校生物競賽人數及分數在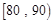 之間的頻數,并計算頻率分布直方圖中
之間的頻數,并計算頻率分布直方圖中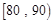 間的矩形的高;
間的矩形的高;
(2)若要從分數在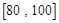 之間的學生中任選兩人進行某項研究,求至少有一人分數在
之間的學生中任選兩人進行某項研究,求至少有一人分數在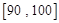 之間的概率.
之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
生產A,B兩種元件,其質量按測試指標劃分為:指標大于或等于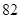 為正品,小于
為正品,小于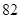 為次品.現隨機抽取這兩種元件各
為次品.現隨機抽取這兩種元件各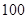 件進行檢測,檢測結果統計如下:
件進行檢測,檢測結果統計如下:
| 測試指標 | 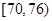 | 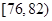 | 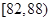 | 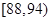 | 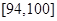 |
| 元件A | 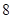 | 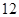 | 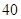 | 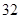 | 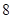 |
| 元件B | 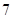 | 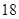 | 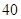 | 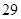 | 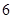 |
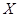 為生產1件元件A和1件元件B所得的總利潤,求隨機變量
為生產1件元件A和1件元件B所得的總利潤,求隨機變量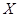 的分布列和數學期望;
的分布列和數學期望;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
我區高三期末統一測試中某校的數學成績分組統計如下表:
| 分組 | 頻數 | 頻率 |
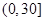 | 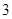 | 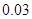 |
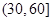 | 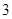 | 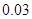 |
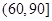 | 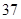 | 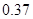 |
 | 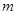 | 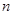 |
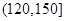 | 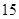 | 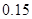 |
| 合計 | 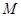 | 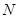 |
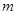 、
、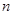 、
、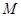 、
、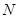 的值,并根據表中所給數據在下面給出的坐標系中畫出頻率分布直方圖;
的值,并根據表中所給數據在下面給出的坐標系中畫出頻率分布直方圖;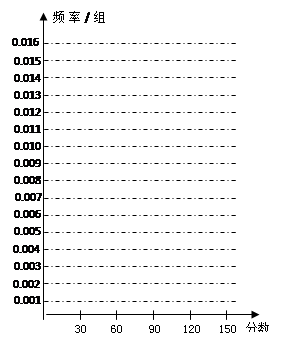
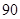 分以上的人數;
分以上的人數;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某食品廠為了檢查甲乙兩條自動包裝流水線的生產情況,隨即在這兩條流水線上各抽取40件產品作為樣本稱出它們的重量(單位:克),重量值落在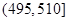 的產品為合格品,否則為不合格品.表1是甲流水線樣本頻數分布表,圖1是乙流水線樣本的頻率分布直方圖.
的產品為合格品,否則為不合格品.表1是甲流水線樣本頻數分布表,圖1是乙流水線樣本的頻率分布直方圖.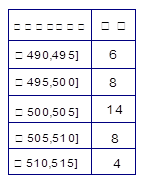
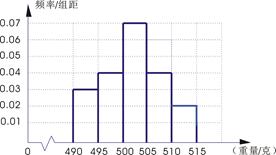
表1:(甲流水線樣本頻數分布表) 圖1:(乙流水線樣本頻率分布直方圖)
(1)根據上表數據在答題卡上作出甲流水線樣本的頻率分布直方圖;
(2)若以頻率作為概率,試估計從兩條流水線分別任取1件產品,該產品恰好是合格品的概率分別是多少;
(3)由以上統計數據完成下面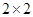 列聯表,并回答有多大的把握認為“產品的包裝質量與兩條自動包裝流水線的選擇有關”.
列聯表,并回答有多大的把握認為“產品的包裝質量與兩條自動包裝流水線的選擇有關”.
| | 甲流水線 | 乙流水線 | 合計 |
| 合格品 | 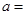 | 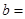 | |
| 不合格品 | 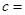 | 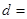 | |
| 合 計 | | |  |
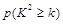 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
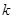 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
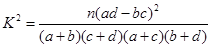 ,其中
,其中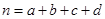 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
袋子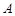 和
和 中裝有若干個均勻的紅球和白球,從
中裝有若干個均勻的紅球和白球,從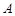 中摸出一個紅球的概率是
中摸出一個紅球的概率是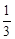 ,從
,從 中摸出一個紅球的概率為
中摸出一個紅球的概率為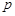 .
.
(1)從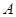 中有放回地摸球,每次摸出一個,共摸4次.
中有放回地摸球,每次摸出一個,共摸4次.
①恰好有2次摸到紅球的概率;②第一次、第三次摸到紅球的概率.
(2)若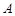 、
、 兩個袋子中的球數之比為4,將
兩個袋子中的球數之比為4,將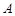 、
、 中的球裝在一起后,從中摸出一個紅球的概率是
中的球裝在一起后,從中摸出一個紅球的概率是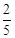 ,求
,求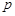 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
工商部門對甲、乙兩家食品加工企業的產品進行深入檢查后,決定對甲企業的5種產品和乙企業的3種產品做進一步的檢驗.檢驗員從以上8種產品中每次抽取一種逐一不重復地進行化驗檢驗.
(1)求前3次檢驗的產品中至少1種是乙企業的產品的概率;
(2)記檢驗到第一種甲企業的產品時所檢驗的產品種數共為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
小王參加一次比賽,比賽共設三關,第一、二關各有兩個必答題,如果每關兩個問題都答對,可進入下一關,第三關有三個問題,只要答對其中兩個問題,則闖關成功.每過一關可一次性獲得價值分別為1000元,3000元,6000元的獎品(不重復得獎),小王對三關中每個問題回答正確的概率依次為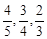 ,且每個問題回答正確與否相互獨立.
,且每個問題回答正確與否相互獨立.
(1)求小王過第一關但未過第二關的概率;
(2)用X表示小王所獲得獎品的價值,寫出X的概率分布列,并求X的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com