
已知函數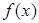 是定義在
是定義在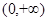 上的單調函數,且對任意的正數
上的單調函數,且對任意的正數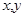 都有
都有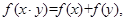 若數列
若數列 的前
的前 項和為
項和為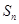 ,且滿足
,且滿足 則
則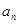 為( )
為( )
A.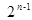 | B.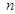 | C.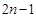 | D.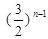 |
D
解析試題分析:因為對任意的正數x,y都有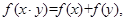
又 ,所以f(sn+2)=f(3)+f(an)=f(3•an),
,所以f(sn+2)=f(3)+f(an)=f(3•an),
因為函數f(x)是定義在(0,+∞)上的單調函數,
所以sn+2=3an………………………………①
當n=1時,s1+2=a1+2=3a1,解得an=1;
當n≥2時,sn-1+2=3an-1………………②
①-②得:an=3an-3an-1
即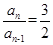 ,所以數列{an}是一個以1為首項,以
,所以數列{an}是一個以1為首項,以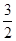 為公比的等比數列,所以
為公比的等比數列,所以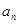 =
=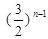 。
。
考點:數列與函數的綜合應用;數列通項公式的求法。
點評:本題以抽象函數為載體考查了等比數列通項公式的求法,其中根據已知得到f(sn+2)=f(3)+f(an)=f(3•an)是解答的關鍵。


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:單選題
定義域為[ ]的函數
]的函數 圖像的兩個端點為A、B,M(x,y)是
圖像的兩個端點為A、B,M(x,y)是 圖象上任意一點,其中
圖象上任意一點,其中 .已知向量
.已知向量 ,若不等式
,若不等式 恒成立, 則稱函數
恒成立, 則稱函數 在[
在[ ]上“k階線性近似”.若函數
]上“k階線性近似”.若函數 在[1,2]上“k階線性近似”,則實數k的取值范圍為( )
在[1,2]上“k階線性近似”,則實數k的取值范圍為( )
A.[0,+∞) B.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com