已知數列{an},記A(n)=a1+a2+a3+…+an,B(n)=a2+a3+a4+…+an+1,C(n)=a3+a4+a5+…+an+2,(n=1,2,3,…),并且對于任意n∈N*,恒有an>0成立.
(1)若a1=1,a2=5,且對任意n∈N*,三個數A(n),B(n),C(n)組成等差數列,求數列{an}的通項公式;
(2)證明:數列{an}是公比為q的等比數列的充分必要條件是:對任意n∈N*,三個數A(n),B(n),C(n)組成公比為q的等比數列.
解:(1)由題意可得2B(n)=A(n)+C(n),
代入可得2(a
2+a
3+a
4+…+a
n+1)=(a
1+a
2+a
3+…+a
n)+(a
2+a
3+a
4+…+a
n+1),
化簡可得
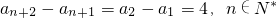
,所以.
∴數列{a
n}的通項公式

(2)(必要性)若數列{a
n}是公比為q的等比數列,
則
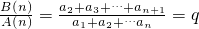
,
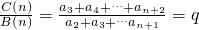
,
所以A(n)、B(n)、C(n)組成公比為q的等比數列.
(充分性):若對于任意n∈N
*,三個數A(n),B(n),C(n)組成公比為q的等比數列,
則B(n)=qA(n),C(n)=qB(n),
于是C(n)-B(n)=q[B(n)-A(n)],得a
n+2-a
2=q(a
n+1-a
1),即a
n+2-qa
n+1=a
2-a
1.
由n=1有B(1)=qA(1),即a
2=qa
1,從而a
n+2-qa
n+1=0.
因為a
n>0,所以

,故數列{a
n}是首項為a
1,公比為q的等比數列.
綜上可得,數列{a
n}是公比為q的等比數列的充要條件是對任意的n∈N
*,都有A(n)、B(n)、C(n)組成公比為q的等比數列.
分析:(1)由等差中項化簡可得
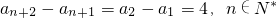
,可得{a
n}為等差數列,進而可得通項公式;
(2)由等比數列的定義,結合題意從充分性和必要性兩方面來證明.
點評:本題以等差數列等比數列為載體,考查充要條件的判斷,屬基礎題.

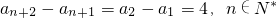 ,所以.
,所以.
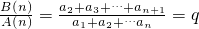 ,
,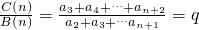 ,
, ,故數列{an}是首項為a1,公比為q的等比數列.
,故數列{an}是首項為a1,公比為q的等比數列.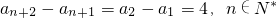 ,可得{an}為等差數列,進而可得通項公式;
,可得{an}為等差數列,進而可得通項公式;

 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案