

 |
 期末好成績系列答案
期末好成績系列答案 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
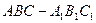 中,
中,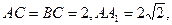 ∠ACB=90°,M是
∠ACB=90°,M是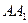 的中點,N是
的中點,N是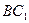 的中點。
的中點。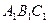 ;
;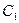 到平面BMC的距離;
到平面BMC的距離;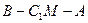 1的大小。
1的大小。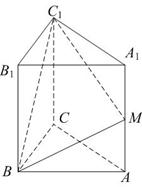
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
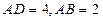 ,E、F分別是線段AB、BC的中點,
,E、F分別是線段AB、BC的中點,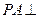 面ABCD. (1)
面ABCD. (1)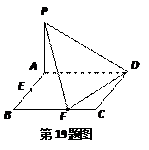 證明:PF⊥FD;
證明:PF⊥FD;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
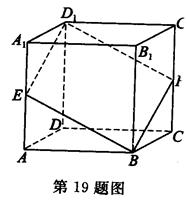
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
,
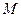 是線段
是線段 的中點.
的中點.
 ;(2)求二面角
;(2)求二面角 的大小;
的大小;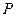 為一動點,若點
為一動點,若點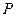 從
從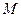 出發(fā),沿棱按照
出發(fā),沿棱按照
 ,求這一過程中形成的三棱錐
,求這一過程中形成的三棱錐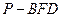 的體積的最小值.
的體積的最小值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
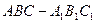 中,
中,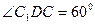 .
.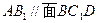 (5分)
(5分)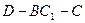 的大小。(7分)
的大小。(7分)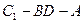 平面角的大小。(7分)
平面角的大小。(7分)查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
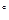 ,在四邊形ABCD中,∠ADC=∠DAB=90
,在四邊形ABCD中,∠ADC=∠DAB=90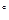 ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.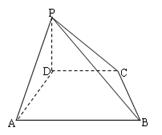
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
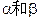 為平面,
為平面,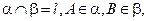 AB=5,A,B在棱l上的射影分別為A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分別為A′,B′,AA′=3,BB′=2.若二面角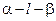 的大小為
的大小為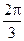 ,求:
,求: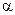 的距離;
的距離;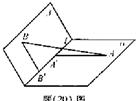
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com