
(本題滿分12)
已知x=1是函數f(x)=m![]() -3(m+1)
-3(m+1)![]() +nx+1的一個極值點,其中m,n
+nx+1的一個極值點,其中m,n![]()
![]() R,m<0.
R,m<0.
(Ⅰ)求m與n的關系表達式; (Ⅱ)求f(x)的單調區間;
(Ⅲ)當x![]()
![]() 時,函數y=f(x)的圖像上任意一點的切線斜率恒大于3m,求m的取值范圍。
時,函數y=f(x)的圖像上任意一點的切線斜率恒大于3m,求m的取值范圍。
解:
(I)f′(x)= 3m![]() -6(m+1)x+n 因為x=1是f(x)的一個極值點,所以f′(1)=0,即 3m-6(m+1)+n=0 所以 n=3m+6. ………………………………3分
-6(m+1)x+n 因為x=1是f(x)的一個極值點,所以f′(1)=0,即 3m-6(m+1)+n=0 所以 n=3m+6. ………………………………3分
(Ⅱ) 由(I)知, f′(x)= 3m![]() -6(m+1)x+3m+6=3m(x-1)[x-(1+
-6(m+1)x+3m+6=3m(x-1)[x-(1+![]() )].
)].
當m<0時,有1>1+![]() .
.
當x變化時,f(x)與f′(x)的變化如下表:
| x | (-∞,1+ | 1+ | (1+ | 1 | (1,∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 單調遞減 | 極小值 | 單調遞增 | 極大值 | 單調遞減 |
由表知,當m<0時,f(x)在(-∞,1+![]() )內單調遞減,在(1+
)內單調遞減,在(1+![]() ,1)內單調遞增,在(1,∞)內單調遞減。 ………………………………7分
,1)內單調遞增,在(1,∞)內單調遞減。 ………………………………7分
(Ⅲ)解法一 由已知條件,得f′(x)﹥3m,即 m![]() -2(m+1)x+2 > 0.
-2(m+1)x+2 > 0.
因為 m < 0,所以 ![]() -
-![]() (m+1)+
(m+1)+![]() < 0,
< 0,
即 ![]() -2(1+
-2(1+![]() )x+
)x+![]() < 0 , x
< 0 , x![]() [-1,1] ①
[-1,1] ①
設g(x)= ![]() -2(1+
-2(1+![]() )x+
)x+![]() ,其函數圖像的開口向上。由題意①式恒成立,
,其函數圖像的開口向上。由題意①式恒成立,
所以{![]()
![]() {
{![]()
![]() {
{![]()
![]() -
-![]()
又m < 0,所以 -![]() < 0,
< 0,
故m的取值范圍是 -![]() < 0. ………………………………12分
< 0. ………………………………12分
解法二 由已知條件,得f′(x)﹥3m,即 3m(x-1)[x-(1+![]() )] > 3m.
)] > 3m.
因為m< 0,所以(x-1)[x-(1+![]() )]< 1 ②
)]< 1 ②
(ⅰ)x=1時,②式化為0 < 1,恒成立,所以m< 0.
(ⅱ)x≠1時,因為 x![]() [-1,1],所以 -2≤x-1<0.
[-1,1],所以 -2≤x-1<0.
②式化為 ![]() <(x-1)-
<(x-1)-![]() , 令t=x-1,則t
, 令t=x-1,則t![]() [-2,0〕.
[-2,0〕.
記 g(t)=t-![]() , 則 g(t)在區間[-2,0〕上是單調增函數,
, 則 g(t)在區間[-2,0〕上是單調增函數,
所以 ![]() =g(-2)=-2-
=g(-2)=-2-![]() =-
=-![]() .
.
由②式恒成立,必有 ![]() < -
< -![]()
![]() -
-![]() < m.
< m.
又m < 0,綜合(ⅰ),(ⅱ)知 -![]() < 0. ………………………………12分
< 0. ………………………………12分


 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源: 題型:
(本題滿分12分)已知![]() 是定義域為[-3,3]的函數,并且設
是定義域為[-3,3]的函數,并且設![]() ,
,![]() ,其中常數c為實數.(1)求
,其中常數c為實數.(1)求![]() 和
和![]() 的定義域;(2)如果
的定義域;(2)如果![]() 和
和![]() 兩個函數的定義域的交集為非空集合,求c的取值范圍;(3)當
兩個函數的定義域的交集為非空集合,求c的取值范圍;(3)當![]() 在其定義域內是奇函數,又是增函數時,求使
在其定義域內是奇函數,又是增函數時,求使![]() 的自變量
的自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2015屆福建省高一寒假作業1數學試卷(解析版) 題型:解答題
(本題滿分12分)
已知直線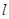 經過直線
經過直線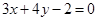 與直線
與直線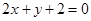 的交點
的交點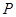 ,且垂直于直線
,且垂直于直線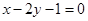 .
.
(Ⅰ)求直線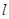 的方程;
的方程;
(Ⅱ)求直線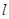 與兩坐標軸圍成的三角形的面積
與兩坐標軸圍成的三角形的面積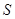 .
.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省高三上學期期中考試文科數學試卷(解析版) 題型:解答題
(本題滿分12分)
已知函數f(x)=x3+ax2+(a+6)x+b(a,b∈R).
(1)若函數f(x)的圖象過原點,且在原點處的切線斜率是3,求a,b的值;
(2) 若f(x)為R上的單調遞增函數,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年遼寧省高三第四次模擬考試理科數學 題型:解答題
(.(本題滿分12分)
已知二次函數 和“偽二次函數”
和“偽二次函數”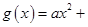
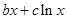 (
(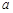 、
、 、
、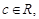
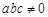 ),
),
(I)證明:只要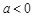 ,無論
,無論 取何值,函數
取何值,函數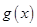 在定義域內不可能總為增函數;
在定義域內不可能總為增函數;
(II)在二次函數 圖象上任意取不同兩點
圖象上任意取不同兩點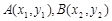 ,線段
,線段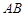 中點的橫坐標為
中點的橫坐標為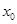 ,記直線
,記直線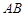 的斜率為
的斜率為 ,
,
(i)求證: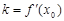 ;
;
(ii)對于“偽二次函數”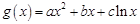 ,是否有(i)同樣的性質?證明你的結論.
,是否有(i)同樣的性質?證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com