
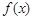 的定義域為
的定義域為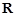 ,
,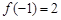 ,對任意
,對任意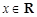 ,
,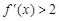 ,則
,則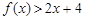 的解集為:
的解集為:A.(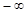 ,+ ,+ ) ) | B.(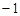 ,1) ,1) |
C.(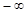 , ,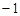 ) ) | D.(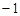 ,+ ,+ ) ) |
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
| 用水量t(單位:噸) | 每噸收費標準(單位:元) |
| 不超過2噸部分 | m |
| 超過2噸不超過4噸部分 | 3 |
| 超過4噸部分 | n |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
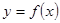 ,其圖像是連續不斷的,且存在常數
,其圖像是連續不斷的,且存在常數 (
(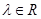 )
)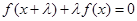 對任意實數
對任意實數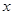 都成立,則稱
都成立,則稱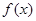 是一個“
是一個“ —伴隨函數”. 有
—伴隨函數”. 有 —伴隨函數”的結論:
—伴隨函數”的結論: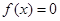 是常數函數中唯一一個“
是常數函數中唯一一個“ —伴隨函數”;
—伴隨函數”;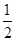 —伴隨函數”至少有一個零點;
—伴隨函數”至少有一個零點;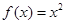 是一個“
是一個“ —伴隨函數”;
—伴隨函數”;| A.1個; | B.2個; | C.3個; | D.0個; |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
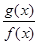 |≤
|≤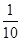 ,則稱f (x)可被g(x)置換,那么下列給出的函數中能置換f (x)=
,則稱f (x)可被g(x)置換,那么下列給出的函數中能置換f (x)=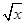 x∈[4,16]的是 ( )
x∈[4,16]的是 ( )| A.g(x)=2x+6 x∈[4,16] | B.g(x)=x2+9 x∈[4,16] |
C.g(x)= 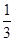 (x+8) x∈[4,16] (x+8) x∈[4,16] | D.g(x)=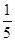 (x+6) x∈[4,16] (x+6) x∈[4,16] |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
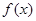 ,若存在區間
,若存在區間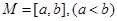 ,使得
,使得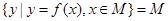 ,則稱區間
,則稱區間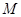 為函數
為函數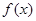 的一個“穩定區間”.現有四個函數:①
的一個“穩定區間”.現有四個函數:①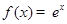 ; ②
; ②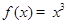 ,
,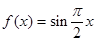 ④
④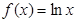 .其中存在“穩定區間”的函數有( )
.其中存在“穩定區間”的函數有( )| A.①② | B.②③ | C.③④ | D.②④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com