(文科做)(本小題滿分16分)
已知橢圓
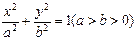
過點
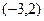
,離心率為
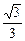
,圓
的圓心為坐標原點,直徑為橢圓的短軸,圓
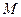
的方程為
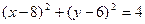
.過圓
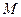
上任一點
作圓
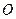
的切線
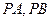
,切點為
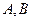
.
(1)求橢圓的方程;
(2)若直線
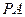
與圓
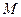
的另一交點為
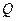
,當弦
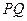
最大時,求直線
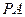
的直線方程;
(3)求
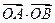
的最值.

因為直線
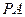
與圓O:

相切,所以

,
解得

或

,…………………………9分
所以,直線
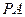
的方程為

或

……………………10分
(3)設(shè)

,
則
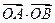
=10

=

=

,………………14分
因為OM=10,所以

,
所以,
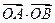
的最大值為

,
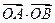
的最小值為

………………………16分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知

的頂點A、B在橢圓

,點

在直線

上,且

(1)當AB邊通過坐標原點O時,求

的面積;
(2)當

,且斜邊AC的長最大時,
求AB所在直線的方程。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分15分) 如圖,橢圓C:
x2+3
y2=3
b2 (
b>0).
(Ⅰ) 求橢圓C的離心率;
(Ⅱ) 若
b=1,
A,
B是橢圓C上兩點,且|
AB | =
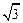
,求△
AOB面積的最大值.
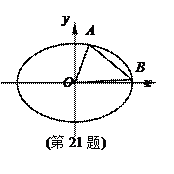
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設(shè)
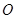
為坐標原點,
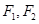
是橢圓
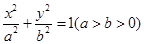
的左、右焦點,若在橢圓上存在點
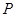
滿足
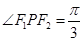
,且
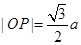
,則該橢圓的離心率為( ▲ )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知橢圓
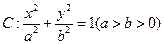
經(jīng)過點M(-2,-1),離心率為
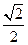
。過點M作傾斜角
互補的兩條直線分別與橢圓C交于異于M的另外兩點P、Q。
(I)求橢圓C的方程;
(II)
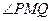
能否為直角?證明你的結(jié)論;
(III)證明:直線PQ的斜率為定值,并

求這個定值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知點
F,
A分別是橢圓
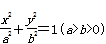
的左焦點、右頂點,
B(0,
b)滿足
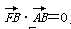
,則橢圓的離心率等于( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
兩個正數(shù)
a、
b的等差中項是
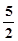
,一個等比中項是
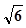
,且
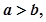
則橢圓
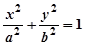
的離心率
e等于( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知橢圓的中心在原點,一個焦點為

,且長軸長是短軸長的2倍,則該橢圓的標準方程是________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若橢圓的短軸為AB,它的一個焦點為F1,則滿足△ABF1為等邊三角形的橢圓的離心率是 .
查看答案和解析>>

 過點
過點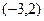 ,離心率為
,離心率為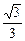 ,圓
,圓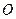 的圓心為坐標原點,直徑為橢圓的短軸,圓
的圓心為坐標原點,直徑為橢圓的短軸,圓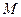 的方程為
的方程為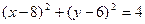 .過圓
.過圓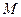 上任一點
上任一點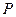 作圓
作圓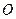 的切線
的切線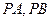 ,切點為
,切點為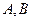 .
.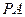 與圓
與圓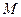 的另一交點為
的另一交點為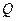 ,當弦
,當弦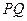 最大時,求直線
最大時,求直線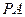 的直線方程;
的直線方程;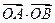 的最值.
的最值. 的頂點A、B在橢圓
的頂點A、B在橢圓 ,點
,點 在直線
在直線 上,且
上,且
 的面積;
的面積; ,且斜邊AC的長最大時,
,且斜邊AC的長最大時,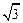 ,求△AOB面積的最大值.
,求△AOB面積的最大值.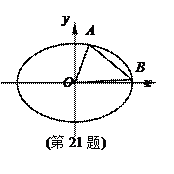
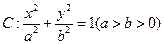 經(jīng)過點M(-2,-1),離心率為
經(jīng)過點M(-2,-1),離心率為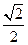 。過點M作傾斜角
。過點M作傾斜角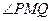 能否為直角?證明你的結(jié)論;
能否為直角?證明你的結(jié)論; 求這個定值。
求這個定值。