
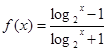 ,若
,若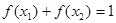 (其中
(其中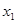 、
、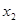 均大于2),則
均大于2),則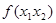 的最小值為 。
的最小值為 。 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
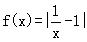
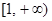 上的單調(diào)性,并證明你的結論;
上的單調(diào)性,并證明你的結論;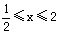 },B=[0,1], 試判斷A與B的關系;
},B=[0,1], 試判斷A與B的關系;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
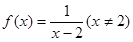 ,則
,則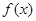 ( )
( )A.在(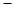 2,+ 2,+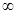 )上是增函數(shù) )上是增函數(shù) | B.在(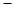 2,+ 2,+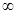 )上是減函數(shù) )上是減函數(shù) |
C.在(2,+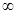 )上是增函數(shù) )上是增函數(shù) | D.在(2,+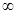 )上是減函數(shù) )上是減函數(shù) |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
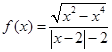 .給出函數(shù)
.給出函數(shù)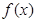 下列性質(zhì):⑴
下列性質(zhì):⑴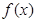 的定義域和值域均為
的定義域和值域均為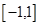 ;⑵
;⑵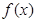 是奇函數(shù);⑶函數(shù)在定義域上單調(diào)遞增;⑷函數(shù)
是奇函數(shù);⑶函數(shù)在定義域上單調(diào)遞增;⑷函數(shù)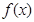 有兩零點;⑸
有兩零點;⑸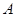 、
、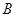 為函數(shù)
為函數(shù)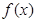 圖象上任意不同兩點,則
圖象上任意不同兩點,則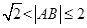 .則函數(shù)
.則函數(shù)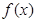 有關性質(zhì)中正確描述的個數(shù)是( )
有關性質(zhì)中正確描述的個數(shù)是( )A.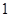 | B.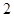 | C.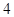 | D.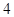 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
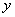 軸相交; ②定義在
軸相交; ②定義在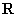 上的奇函數(shù)
上的奇函數(shù)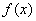 必滿足
必滿足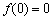 ;
;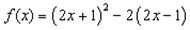 既不是奇函數(shù)又不是偶函數(shù);
既不是奇函數(shù)又不是偶函數(shù);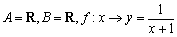 ,則
,則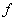 為
為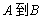 的映射;
的映射;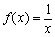 在
在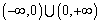 上是減函數(shù).
上是減函數(shù).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
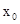 ,使得對于任意
,使得對于任意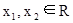 ,
,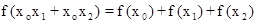 恒成立.
恒成立.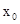 的值;
的值;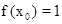 ,且對任意正整數(shù)n,有
,且對任意正整數(shù)n,有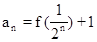 ,又數(shù)列
,又數(shù)列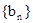 滿足
滿足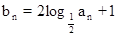 ,求
,求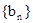 的通項公式.
的通項公式.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
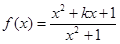 。
。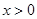 時,
時,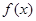 的最小值為-1,求實數(shù)k的值;
的最小值為-1,求實數(shù)k的值; ,均存在以
,均存在以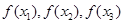 為三邊邊長的三角形,求實數(shù)k的取值范圍。
為三邊邊長的三角形,求實數(shù)k的取值范圍。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.a(chǎn)≥-3 | B.a(chǎn)≤-3 |
| C.a(chǎn)≤5 | D.a(chǎn)≥3 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com