
(本題滿分15分)如圖,分別過橢圓E: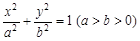 左右焦點
左右焦點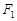 、
、 的動直線l1、l2相交于P點,與橢圓E分別交于A、B與C、D不同四點,直線OA、OB、OC、OD的斜率
的動直線l1、l2相交于P點,與橢圓E分別交于A、B與C、D不同四點,直線OA、OB、OC、OD的斜率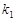 、
、 、
、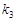 、
、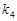 滿足
滿足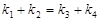 .已知當(dāng)l1與x軸重合時,
.已知當(dāng)l1與x軸重合時,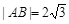 ,
,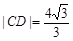 .
.
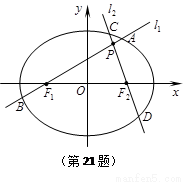
(Ⅰ)求橢圓E的方程;
(Ⅱ)是否存在定點M、N,使得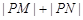 為定值.若存在,求出M、N點坐標(biāo),若不存在,說明理由.
為定值.若存在,求出M、N點坐標(biāo),若不存在,說明理由.
(Ⅰ) .
.
(Ⅱ)存在點M、N其坐標(biāo)分別為(0
, -1)、(0, 1),使得 為定值
為定值 .
.
【解析】本試題主要是考查了橢圓方程的求解,以及直線與橢圓的位置關(guān)系的綜合運用。
(1)利用已知中的線段的長度得到a,b,c的關(guān)系式,進而求解得到橢圓的方程。
(2)設(shè)出直線與橢圓聯(lián)立,利用韋達定理來表示坐標(biāo)關(guān)系,同時利用斜率的知識求解得到參數(shù)的關(guān)系式,進而證明定值。
解(Ⅰ)當(dāng)l1與x軸重合時,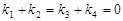 ,即
,即 ,(2分)
,(2分)
∴ l2垂直于x軸,得 ,
, ,(4分)
,(4分)
得 ,
, , ∴ 橢圓E的方程為
, ∴ 橢圓E的方程為 .(6分)
.(6分)
(Ⅱ)焦點 、
、 坐標(biāo)分別為(-1, 0)、(1, 0).
坐標(biāo)分別為(-1, 0)、(1, 0).
當(dāng)直線l1或l2斜率不存在時,P點坐標(biāo)為(-1, 0)或(1, 0).
當(dāng)直線l1、l2斜率存在時,設(shè)斜率分別為 ,
, ,設(shè)
,設(shè) ,
, ,
,
由 得
得  ,
,
∴  ,
, .(8分)
.(8分)

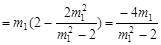 ,(10分)
,(10分)
同理
 .
.
∵ , ∴
, ∴ ,即
,即 .
.
由題意知 , ∴
, ∴ .(12分)
.(12分)
設(shè) ,則
,則 ,即
,即 ,(14分)
,(14分)
由當(dāng)直線l1或l2斜率不存在時,P點坐標(biāo)為(-1, 0)或(1, 0)也滿足,
∴ 點橢圓
點橢圓 上,
上,
∴ 存在點M、N其坐標(biāo)分別為(0 , -1)、(0, 1),使得 為定值
為定值 .(15分)
.(15分)


 名師導(dǎo)航單元期末沖刺100分系列答案
名師導(dǎo)航單元期末沖刺100分系列答案 名校名卷單元同步訓(xùn)練測試題系列答案
名校名卷單元同步訓(xùn)練測試題系列答案科目:高中數(shù)學(xué) 來源: 題型:
|
設(shè)![]() 的夾角為
的夾角為![]()
的取值范圍; (III)設(shè)以點N(0,m)為圓心,以![]() 為
為
半徑的圓與曲線E在第一象限的交點H,若圓在點H處的
切線與曲線E在點H處的切線互相垂直,求實數(shù)m的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年浙江省溫州八校高三9月期初聯(lián)考文科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分15分)如圖,在四棱錐 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, 與平面
與平面 所成角的正切值依次是
所成角的正切值依次是 和
和 ,
, ,
, 依次是
依次是 的中點.
的中點.
(Ⅰ)求證: ;
;
(Ⅱ)求直線 與平面
與平面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年浙江省杭州市高三寒假作業(yè)數(shù)學(xué)卷三 題型:解答題
(本題滿分15分)如圖,在矩形ABCD中,點E,F(xiàn)分別在線段AB,AD上,AE=EB=AF= 沿直線EF將
沿直線EF將 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF.
(I)求二面角 的余弦值;
的余弦值;
(II)點M,N分別在線段FD,BC上,若沿直線MN將四邊形MNCD向上翻折,使C
與 重合,求線段FM的長.
重合,求線段FM的長.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年江蘇省高三年級隨堂練習(xí)數(shù)學(xué)試卷 題型:解答題
(本題滿分15分)
如圖:某污水處理廠要在一個矩形污水處理池 的池底水平鋪設(shè)污水凈化管道
的池底水平鋪設(shè)污水凈化管道 ,
, 是直角頂點)來處理污水,管道越長,污水凈化效果越好.設(shè)計要求管道的接口
是直角頂點)來處理污水,管道越長,污水凈化效果越好.設(shè)計要求管道的接口 是
是 的中點,
的中點, 分別落在線段
分別落在線段 上.已知
上.已知 米,
米, 米,記
米,記 .
.
(Ⅰ)試將污水凈化管道的長度 表示為
表示為 的函數(shù),并寫出定義域;
的函數(shù),并寫出定義域;
(Ⅱ)問:當(dāng) 取何值時,污水凈化效果最好?并求出此時管道的長度.
取何值時,污水凈化效果最好?并求出此時管道的長度.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年普通高等學(xué)校招生全國統(tǒng)一考試(浙江卷)理科數(shù)學(xué) 題型:解答題
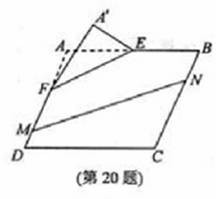 本題滿分15分)如圖, 在矩形
本題滿分15分)如圖, 在矩形 中,點
中,點 分別
分別
在線段 上,
上, .沿直線
.沿直線
將  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)點 分別在線段
分別在線段 上,若沿直線
上,若沿直線 將四
將四
邊形 向上翻折,使
向上翻折,使 與
與 重合,求線段
重合,求線段
的長。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com