（14分）
已知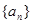
是等差數列，其前n項和為Sn，已知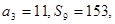
（1）求數列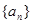的通項公式；
（2）設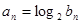
，證明
是等比數列，并求其前n項和Tn.
一課一練課時達標系列答案科目：高中數學 來源：2015屆遼寧省東北育才雙語學校高一下學期期中考試數學試卷（解析版） 題型：解答題
已知{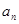
}是等差數列，其前
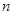項和為
，{
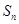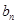}是等比數列,且
=
，
，
.
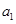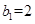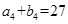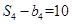（1）求數列{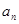}與{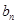}的通項公式；
（2）記
，求滿足不等式
的最小正整數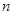的值.
查看答案和解析>>
科目：高中數學 來源：2012-2013學年浙江省寧波市金蘭合作組織高三上學期期中聯考文科數學試卷（解析版） 題型：解答題
（本題14分）已知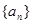
是等差數列，其前n項和為Sn，
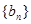是等比數列，且
，
.
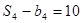（Ⅰ）求數列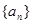與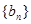的通項公式；
（Ⅱ）記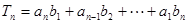
，
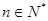，求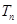
（）.
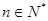查看答案和解析>>
科目：高中數學 來源：2014屆廣東佛山市高一第一段考數學試卷（解析版） 題型：解答題
已知
是等差數列，其前n項和為Sn，已知
（1）求數列的通項公式；
（2）設
，證明
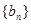是等比數列，并求其前n項和Tn.
查看答案和解析>>
科目：高中數學 來源：2012年全國普通高等學校招生統一考試文科數學（天津卷解析版） 題型：解答題
已知
是等差數列，其前n項和為
， 
是等比數列，且
（I）求數列與的通項公式；
（II）記
求證：
,
。
【考點定位】本小題主要考查等差數列與等比數列的概念、通項公式、前n項和公式、數列求和等基礎知識.考查化歸與轉化的思想方法.考查運算能力、推理論證能力.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
解得
，
。
得
，因為
，
是等差數列，其前n項和為
，已知
求數列