
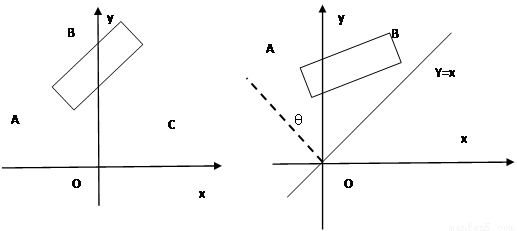
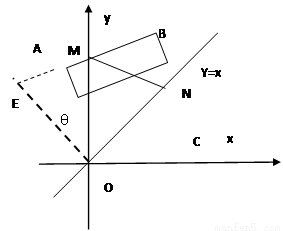
如圖1,在平面直角坐標系中,邊長為1的正方形OABC的頂點B在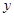 軸的正半軸上,O為坐標原點.現將正方形OABC繞O點按順時針方向旋轉.
軸的正半軸上,O為坐標原點.現將正方形OABC繞O點按順時針方向旋轉.
(1)當點A第一次落到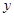 軸正半軸上時,求邊BC在旋轉過程中所掃過的面積;
軸正半軸上時,求邊BC在旋轉過程中所掃過的面積;
(2)若線段AB與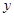 軸的交點為M(如圖2),線段BC與直線
軸的交點為M(如圖2),線段BC與直線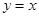 的交點為N.設
的交點為N.設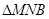 的周長為
的周長為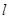 ,在正方形OABC旋轉的過程中
,在正方形OABC旋轉的過程中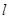 值是否有改變?并說明你的結論;
值是否有改變?并說明你的結論;
(3)設旋轉角為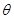 ,當
,當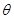 為何值時,
為何值時,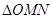 的面積最小?求出這個最小值, 并求出此時△BMN的內切圓半徑.
的面積最小?求出這個最小值, 并求出此時△BMN的內切圓半徑.

(1)S= 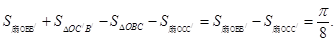
(2) 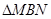 的周長為定值2. (3)
的周長為定值2. (3)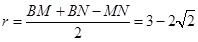 .
.
【解析】此題主要考查了一次函數的綜合應用以及根的判別式、全等三角形的判定與性質、扇形面積求法等知識,利用圖形旋轉的變化規律得出對應邊之間關系是解題關鍵
(1)根據正方形的性質得出∠AOB=∠BOC=45°,BO=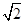 ,再利用S=S扇形OBB′+S△OC′B′-S△OCB-S扇形OCC′=S扇形OBB′-S扇形OCC′求出即可;
,再利用S=S扇形OBB′+S△OC′B′-S△OCB-S扇形OCC′=S扇形OBB′-S扇形OCC′求出即可;
(2)首先延長BA交直線y=-x于E點,Rt△AEO≌Rt△CNO,得出AE=CN,OE=ON,進而得出△MOE≌△MON,得出ME=MN,進而得出l的值不變;
(3)設MN=m,AM=t.由(2)知,在Rt△MNB中,MN2=MB2+NB2,利用 MN+MB+NB=2,得出m2=(1-t)2+(2-m-1+t)2,即可得出m的取值范圍,即可得出,△OMN的面積最小值,再利用直角三角形內切圓半徑求法得出答案即可
解:(1)設旋轉后C在 、B在
、B在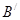 、A在
、A在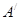 .
.
S= 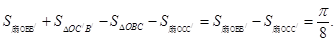 ………….4分
………….4分
(2)延長BA交直線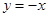 于E點,在
于E點,在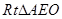 與
與 中,
中,
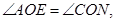
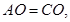 所以
所以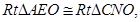 所以
所以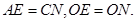
又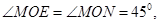 所以
所以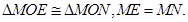
所以 故
故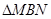 的周長為定值2.…..10分
的周長為定值2.…..10分
(3)因為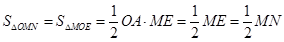 ,
,
設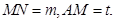 由(2)知,在
由(2)知,在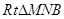 中,
中,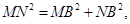
因為 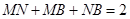 ,所以
,所以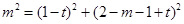 ,得:
,得: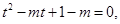
因為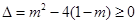 ,所以
,所以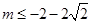 (舍去)或
(舍去)或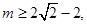
所以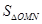 的最小值為
的最小值為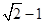 .
…….13分
.
…….13分
此時△=0 ∴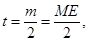 ∴A為ME的中點.
∴A為ME的中點.
又因為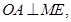 所以OA是
所以OA是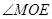 的平分線,
的平分線,
所以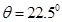 . ……15分
. ……15分
在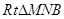 中,
中,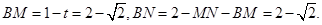 設
設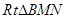 的內切圓半徑為r,所以
的內切圓半徑為r,所以 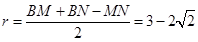 .
……18分
.
……18分


科目:高中數學 來源: 題型:

若折痕所在直線的斜率為k,試寫出折痕所在直線的方程;
查看答案和解析>>
科目:高中數學 來源: 題型:

若折痕所在直線的斜率為k,試寫出折痕所在直線的方程;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com