Question

稱一個函數是“好函數”當且僅當其滿足：定義在上；存在，使其在上單調遞增，在上單調遞減，則以下函數是“好函數”的有 ．
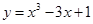?；?；?；④

Answer 1

.②③

解析試題分析：解：①中函數y=|x-2|定義域為R，y=|x-2|= ∴不存在a，使y=|x-2|在（-∞，a）上單調遞增，故不正確；②中函數y=x|x-2|定義域為R，y=x|x-2|=y=x|x-2|在（-∞，1）、（2，+∞）上單調遞增，在（1，2）上單調遞減，滿足好函數的定義，故正確；③中函數y=x³-x+1定義域為R，則y′=3x²-1＜0解得x∈（- ，），y′=3x²-1＞0解得x∈（-∞，-）∪（，+∞），∴y=x³-x+1在（-∞，-）、（，+∞）上單調遞增，在（-，）上單調遞減，滿足好函數的定義，故正確；④中函數y=x³+x+3定義域為R，則y′=3x²+1＞0恒成立，故不存在a＜b，使函數y=x³+x+3在（a，b）上單調遞減，不滿足好函數的定義，故不正確；故答案為：②③
考點：導數研究函數的單調性
點評：本題主要考查了利用導數研究函數的單調性，以及絕對值函數的處理方法和新定義，同時考查了轉化的思想，屬于中檔題