
已知四邊形![]() 為菱形,
為菱形,![]() ,兩個正三棱錐
,兩個正三棱錐![]() (底面是正三角形且頂點在底面上的射影是底面正三角形的中心)的側棱長都相等,點
(底面是正三角形且頂點在底面上的射影是底面正三角形的中心)的側棱長都相等,點![]() 分別在
分別在![]() 上,且
上,且![]() .
.
(Ⅰ)求證:![]() ;
;
(Ⅱ)求平面![]() 與底面
與底面![]() 所成銳二面角的平面角的正切值;
所成銳二面角的平面角的正切值;
(Ⅲ)求多面體![]() 的體積.
的體積.

(Ⅰ) 見解析(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
(Ⅰ)取![]() 中點
中點![]() ,連
,連![]() 、
、![]() ,則
,則![]()

![]() 面
面![]() ,
,![]()
![]()
![]()
![]()
![]()
又![]()
![]() ……………3分
……………3分
(Ⅱ)設![]() 在底面的射影分別為
在底面的射影分別為![]() ,則
,則
由所給的三棱錐均為正三棱錐且兩三棱錐全等,
故![]() ∥
∥![]() ,且
,且![]() =
=![]() ,∴四邊形
,∴四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ∥
∥![]() ,又
,又![]() 分別為△
分別為△![]() ,△
,△![]() 的中心,
的中心,
∴![]() 在菱形的對角線
在菱形的對角線![]() 上,
上,
∴![]() ∥
∥![]() ,即
,即![]() ∥平面
∥平面![]() …………………………………5分
…………………………………5分
設平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,取
,取![]() 中點
中點![]() 連結
連結![]() ,
,
由
∴![]() 為平面
為平面![]() 與平面
與平面![]() 所成二面角的平面角
所成二面角的平面角
…………………………7分
在![]() △
△![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ……………………………9分
……………………………9分
(Ⅲ設![]() 、
、![]() 在
在![]() 和
和![]() 上的射影為
上的射影為![]() ,則
,則![]() 均在直線
均在直線![]() 上,且
上,且![]() 為平行四邊形,
為平行四邊形,![]() 。
。
| |
設![]() ,則
,則![]() ,又
,又![]() ,由(1)知
,由(1)知![]()
![]() 即
即![]()
![]() 面
面![]() ,
,![]() ,又
,又![]() 面
面![]() 。
。
設![]() 四棱錐
四棱錐![]() 的高為
的高為![]() ,且
,且![]()

![]()
![]() 在
在![]() 中,
中,
|
![]()
![]() ……………13分
……………13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
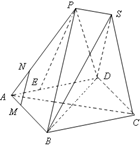 已知四邊形ABCD為菱形,AB=6,∠BAD=60°,兩個正三棱錐P-ABD、S-BCD(底面是正三角形且頂點在底面上的射影是底面正三角形的中心)的側棱長都相等,如圖,E、M、N分別在AD、
已知四邊形ABCD為菱形,AB=6,∠BAD=60°,兩個正三棱錐P-ABD、S-BCD(底面是正三角形且頂點在底面上的射影是底面正三角形的中心)的側棱長都相等,如圖,E、M、N分別在AD、| 1 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年東城區二模理)(13分)
如圖,![]() 為雙曲線
為雙曲線![]()
![]() 的右焦點,
的右焦點,
![]() 為雙曲線
為雙曲線![]() 右支上一點,且位于
右支上一點,且位于![]() 軸上方,
軸上方,![]() 為左準線上一點,
為左準線上一點,![]() 為坐標原點.已知四邊形
為坐標原點.已知四邊形![]() 為菱形.
為菱形.
(Ⅰ)求雙曲線![]() 的離心率
的離心率![]() ;
;
(Ⅱ)若經過焦點![]() 且平行于
且平行于![]() 的直線交雙曲線于
的直線交雙曲線于![]() 兩點,且
兩點,且![]() ,求此時的雙曲線方程.
,求此時的雙曲線方程.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com