
在區間【- ,
, 】內隨機取兩個數分別記作a,b。則使得函數
】內隨機取兩個數分別記作a,b。則使得函數 =
=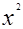 +
+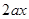 -
- +
+ 有零點的概率為 ( )
有零點的概率為 ( )
A. | B. | C.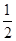 | D. |
B
解析試題分析:先判斷概率的類型,由題意知本題是一個幾何概型,由a,b使得函數f(x)=x2+2ax-b2+π有零點,得到關于a、b的關系式,寫出試驗發生時包含的所有事件和滿足條件的事件,做出對應的面積,求比值得到結果.解:由題意知本題是一個幾何概型,∵a,b使得函數f(x)=x2+2ax-b2+π有零點,∴△≥0,∴a2+b2≥π,試驗發生時包含的所有事件是Ω={(a,b)|-π≤a≤π,-π≤b≤π}∴S=(2π)2=4π2,而滿足條件的事件是{(a,b)|a2+b2≥π},∴s=4π2-π2=3π2,由幾何概型公式得到P= 故選B.
故選B.
考點:幾何概型
點評:高中必修中學習了幾何概型和古典概型兩種概率問題,先要判斷該概率模型是不是古典概型,再要找出隨機事件A包含的基本事件的個數和試驗中基本事件的總數.再看是不是幾何概型,它的結果要通過長度、面積或體積之比來得到.


科目:高中數學 來源: 題型:單選題
如圖所示,邊長為2的正方形中有一封閉曲線圍成的陰影區域,在正方形中隨機撒一粒豆子,它落在陰影區域內的概率是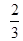 ,則陰影區域的面積為( )
,則陰影區域的面積為( ) 
A. | B. | C.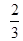 | D.無法計算 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
從只含有二件次品的10個產品中取出三件,設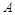 為“三件產品全不是次品”,
為“三件產品全不是次品”,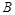 為“三件產品全是次品”,
為“三件產品全是次品”,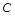 為“三件產品不全是次品”,則下列結論正確的是:
為“三件產品不全是次品”,則下列結論正確的是:
A.事件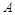 與 與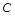 互斥 互斥 | B.事件C是隨機事件 |
| C.任兩個均互斥 | D.事件B是不可能事件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com