
| 1 |
| 2 |
| 1 |
| a12 |
| 1 |
| a22 |
| 1 |
| a32 |
| 1 |
| an2 |
| 7 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| S1 | ||
|
| 1 |
| an2 |
| 1 |
| n2 |
| 1 |
| (n-1)n |
| 1 |
| (n-1) |
| 1 |
| n |
|
| 1 |
| a12 |
| 7 |
| 4 |
| 1 |
| a12 |
| 1 |
| a22 |
| 5 |
| 4 |
| 7 |
| 4 |
| 1 |
| a12 |
| 1 |
| a22 |
| 1 |
| a32 |
| 1 |
| an2 |
| 7 |
| 4 |


科目:高中數(shù)學(xué) 來源:湖南省師大附中2010屆高三第三次月考(理) 題型:解答題
設(shè)數(shù)列 的前
的前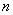 項和為
項和為 ,如果
,如果 為常數(shù),則稱數(shù)列
為常數(shù),則稱數(shù)列 為“科比數(shù)列”.
為“科比數(shù)列”.
(Ⅰ)已知等差數(shù)列 的首項為1,公差不為零,若
的首項為1,公差不為零,若 為“科比數(shù)列”,求
為“科比數(shù)列”,求 的通項公式;
的通項公式;
(Ⅱ)設(shè)數(shù)列 的各項都是正數(shù),前
的各項都是正數(shù),前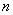 項和為
項和為 ,若
,若 對任意
對任意 都成立,試推斷數(shù)列
都成立,試推斷數(shù)列 是否為“科比數(shù)列”?并說明理由.
是否為“科比數(shù)列”?并說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com