
已知三次函數y = f (x)過點(–1,0),且f ′(x) = (x + 1)2,將y = f (x)的圖象向右平移一個單位,再將各點的縱坐標變為原來的3倍得函數y = g (x)的圖象,函數y = h (x)與y = g (x)的圖象關于點M(2,0)對稱.
(1)求y = h (x)的解析式;
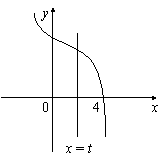 (2)若直線x = t
(0<t<4)將函數y = h (x)的圖象與兩坐標軸圍成的圖形的面積二等分,求t的值.
(2)若直線x = t
(0<t<4)將函數y = h (x)的圖象與兩坐標軸圍成的圖形的面積二等分,求t的值.
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:湖南省長沙市一中2010屆高三上學期第二次月考(數學理) 題型:044
已知三次函數y=f(x)過點(-1,0),且![]() (x)=(x+1)2,將y=f(x)的圖象向右平移一個單位,再將各點的縱坐標變為原來的3倍得函數y=g(x)的圖象,函數y=h(x)與y=g(x)的圖象關于點M(2,0)對稱.
(x)=(x+1)2,將y=f(x)的圖象向右平移一個單位,再將各點的縱坐標變為原來的3倍得函數y=g(x)的圖象,函數y=h(x)與y=g(x)的圖象關于點M(2,0)對稱.

(1)求y=h(x)的解析式;
(2)若直線x=t(0<t<4)將函數y=h(x)的圖象與兩坐標軸圍成的圖形的面積二等分,求t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com