

 時,
時, 在
在 單調遞減,在
單調遞減,在 單調遞增,在
單調遞增,在 上單調遞減.
上單調遞減. )及(-
)及(-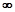 ,1)上單調遞增;在(1,1+
,1)上單調遞增;在(1,1+ )上單調遞減 .
)上單調遞減 . 的取值范圍為
的取值范圍為
 因為
因為 是函數
是函數 的一個極值點,所以
的一個極值點,所以 ,即
,即 ,所以
,所以
 上為增函數,在(6,+
上為增函數,在(6,+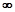 )上為減函數
)上為減函數 =
=
 時,有
時,有 ,當
,當 變化時,
變化時, 與
與 的變化如下表:
的變化如下表: |  |  |  | 1 |  |
 |  | 0 |  | 0 |  |
| | | | | | |
 | 調調遞減 | 極小值 | 單調遞增 | 極大值 | 單調遞減 |
 時,
時, 在
在 單調遞減,在
單調遞減,在 單調遞增,在
單調遞增,在 上單調遞減.
上單調遞減. )及(-
)及(-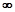 ,1)上單調遞增;在(1,1+
,1)上單調遞增;在(1,1+ )上單調遞減 .
)上單調遞減 . ,即
,即
 所以
所以 即
即 ①
① ,其函數開口向上,由題意知①式恒成立,
,其函數開口向上,由題意知①式恒成立,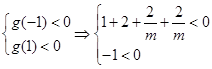 解之得
解之得 又
又 所以
所以
 的取值范圍為
的取值范圍為


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com