
(本題滿分14分) 本題共有2個小題,第1小題滿分6分,第2小題滿分8分.
(文)某種型號汽車的四個輪胎半徑相同,均為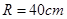 ,該車的底盤與輪胎中心在同一水平面上. 該車的涉水安全要求是:水面不能超過它的底盤高度. 如圖所示:某處有一“坑形”地面,其中坑
,該車的底盤與輪胎中心在同一水平面上. 該車的涉水安全要求是:水面不能超過它的底盤高度. 如圖所示:某處有一“坑形”地面,其中坑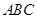 形成頂角為
形成頂角為 的等腰三角形,且
的等腰三角形,且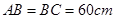 ,如果地面上有
,如果地面上有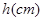 (
( )高的積水(此時坑內(nèi)全是水,其它因素忽略不計).
)高的積水(此時坑內(nèi)全是水,其它因素忽略不計).
(1)當輪胎與 、
、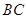 同時接觸時,求證:此輪胎露在水面外的高度(從輪胎最上部到水面的距離)為
同時接觸時,求證:此輪胎露在水面外的高度(從輪胎最上部到水面的距離)為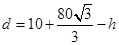 ;
;
(2) 假定該汽車能順利通過這個坑(指汽車在過此坑時,符合涉水安全要求),求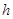 的最大值.
的最大值.
(精確到1cm).
(1)當輪胎與 、
、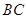 同時接觸時,求出此輪胎露在水面外的高度即可證明
同時接觸時,求出此輪胎露在水面外的高度即可證明
(2)16cm
解析試題分析: (1) 當輪胎與AB、BC同時接觸時,設(shè)輪胎與AB邊的切點為T,輪胎中心為O,則|OT|=40,由∠ABC=1200,知∠OBT=600, ……2分
故|OB|=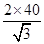 . ……4分
. ……4分
所以,從B點到輪胎最上部的距離為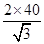 +40, ……6分
+40, ……6分
此輪胎露在水面外的高度為d=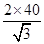 +40-(
+40-(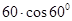 +h)=
+h)=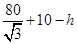 ,
,
從而得證. ……8分
(2)只要d 40, ……12分
40, ……12分
即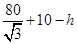
 40,解得h
40,解得h 16cm.,所以h的最大值為16cm. ……14分
16cm.,所以h的最大值為16cm. ……14分
考點:本小題主要考查函數(shù)在實際問題中的應(yīng)用,考查學(xué)生由實際問題向數(shù)學(xué)問題轉(zhuǎn)化的能力和運算求解能力.
點評:解決實際應(yīng)用題的關(guān)鍵是認真讀題,正確將實際問題轉(zhuǎn)化為熟悉的數(shù)學(xué)問題.


科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,扇形 是一個觀光區(qū)的平面示意圖,其中
是一個觀光區(qū)的平面示意圖,其中 ,半徑
,半徑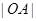 =1
=1 ,為了便于游客觀光休閑,擬在觀光區(qū)內(nèi)鋪設(shè)一條從入口
,為了便于游客觀光休閑,擬在觀光區(qū)內(nèi)鋪設(shè)一條從入口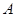 到出口
到出口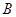 的觀光道路,道路由弧
的觀光道路,道路由弧 ,線段
,線段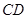 及線段
及線段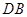 組成,其中
組成,其中 在線段
在線段 上且
上且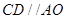 ,設(shè)
,設(shè)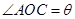

(1)用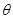 表示
表示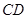 的長度,并寫出
的長度,并寫出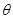 的取值范圍.
的取值范圍.
(2)當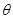 為何值時,觀光道路最長?
為何值時,觀光道路最長?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題14分)已知向量m = ,向量n =
,向量n =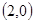 ,且m與n所成角為
,且m與n所成角為 ,其中A、B、C是
,其中A、B、C是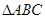 的內(nèi)角。
的內(nèi)角。
(Ⅰ)求角B的大小;
(Ⅱ)求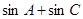 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分10分)在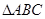 中,
中,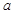 ,
,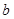 ,
, 分別是三內(nèi)角A,B,C所對的三邊,已知
分別是三內(nèi)角A,B,C所對的三邊,已知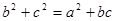 .
.
(1)求角A的大小;
(2)若 ,試判斷
,試判斷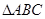 的形狀.
的形狀.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,2012年春節(jié),攝影愛好者S在某公園A處,發(fā)現(xiàn)正前方B處有一立柱,測得立柱頂端O的仰角和立柱底部B的俯角均為 ,已知S的身高約為
,已知S的身高約為 米(將眼睛距地面的距離按
米(將眼睛距地面的距離按 米處理)
米處理)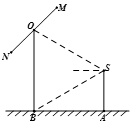
(1) 求攝影者到立柱的水平距離和立柱的高度;
(2) 立柱的頂端有一長2米的彩桿MN繞中點O在S與立柱所在的平面內(nèi)旋轉(zhuǎn).攝影者有一視角范圍為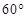 的鏡頭,在彩桿轉(zhuǎn)動的任意時刻,攝影者是否都可以將彩桿全部攝入畫面?說明理由.
的鏡頭,在彩桿轉(zhuǎn)動的任意時刻,攝影者是否都可以將彩桿全部攝入畫面?說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題12分)
在銳角△ABC中,a、b、c分別為角A、B、C所對的邊,且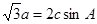
(1)求角C的大小;
(2)若c= ,且△ABC的面積為
,且△ABC的面積為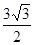
 ,求a+b的值。
,求a+b的值。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com