
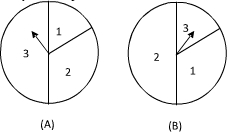
 如圖是兩個獨立的轉盤(A)、(B),在兩個圖中三個扇形區域的圓心角分別為60°、120°、180°.用這兩個轉盤進行玩游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域數為x,轉盤(B)指針所對的區域為y,x、y∈{1,2,3},設x+y的值為ξ,每一次游戲得到獎勵分為ξ
如圖是兩個獨立的轉盤(A)、(B),在兩個圖中三個扇形區域的圓心角分別為60°、120°、180°.用這兩個轉盤進行玩游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域數為x,轉盤(B)指針所對的區域為y,x、y∈{1,2,3},設x+y的值為ξ,每一次游戲得到獎勵分為ξ| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 9 |
| 1 |
| 18 |
| 7 |
| 36 |
| 13 |
| 36 |
| 11 |
| 36 |
| 3 |
| 36 |
| ξ | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 18 |
| 7 |
| 36 |
| 13 |
| 36 |
| 11 |
| 36 |
| 1 |
| 12 |
| 25 |
| 6 |


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
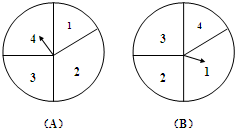 (2010•珠海二模)如圖是兩個獨立的轉盤(A)、(B),在兩個圖中的四個扇形區域的圓心角分別為60°、120°、90°90°.用這兩個轉盤進行玩游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域數為x,轉盤(B)指針所對的區域數為y,x、y∈{1,2,3,4},設x+y的值為ξ,每一次游戲得到獎勵分為ξ.
(2010•珠海二模)如圖是兩個獨立的轉盤(A)、(B),在兩個圖中的四個扇形區域的圓心角分別為60°、120°、90°90°.用這兩個轉盤進行玩游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域數為x,轉盤(B)指針所對的區域數為y,x、y∈{1,2,3,4},設x+y的值為ξ,每一次游戲得到獎勵分為ξ.查看答案和解析>>
科目:高中數學 來源: 題型:
(08年荊州市質檢二) (12分) 如圖是兩個獨立的轉盤![]() ,在兩個圖中三個扇形區域的圓心角分別為
,在兩個圖中三個扇形區域的圓心角分別為![]() 。用這兩個轉盤進行玩游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤
。用這兩個轉盤進行玩游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤![]() 指針所對的區域數為
指針所對的區域數為![]() ,轉盤
,轉盤![]() 指針所對的區域為
指針所對的區域為![]() ,
,![]() ,設
,設![]() 的值為
的值為![]() ,每一次游戲得到獎勵分為
,每一次游戲得到獎勵分為![]()
⑴求![]() 且
且![]() 的概率;
的概率;
⑵某人進行了![]() 次游戲,求他平均可以得到的獎勵分
次游戲,求他平均可以得到的獎勵分
(注:這是一個幾何概率題,幾何概率的基本思想是把事件與幾何區域對應,利用幾何區域的度量來計算事件發生的概率,即事件![]() 的概率
的概率![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
|
(Ⅰ)求![]() <2且
<2且![]() >1的概率;
>1的概率;
(Ⅱ)某人進行了12次游戲,求他平均可以得到的獎勵分.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年重慶市高三5月月考考試理科數學 題型:解答題
(本小題滿分13分)
如圖是兩個獨立的轉盤(A)、(B),在兩個圖中三個扇形區域的圓心角分別為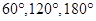 ,用這兩個轉盤進行游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域為x,轉盤(B)指針所對的區域為y,
,用這兩個轉盤進行游戲,規則是:同時轉動兩個轉盤待指針停下(當兩個轉盤中任意一個指針恰好落在分界線時,則這次轉動無效,重新開始),記轉盤(A)指針所對的區域為x,轉盤(B)指針所對的區域為y,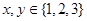 ,設
,設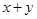 的值為
的值為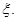
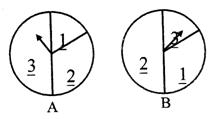
(1)求 的概率;
的概率;
(2)求隨機變量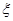 的發布列與數學期望。
的發布列與數學期望。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com