Question

過雙曲線x²-y²=1的右焦點F作直線l交雙曲線于A、B兩點，記雙曲線漸近線的方向向量為v，當在v方向上的投影的絕對值為時，求直線l的方程.

Answer 1

解:由已知，F(xiàn)(,0)，雙曲線的漸近線y=±x的方向向量為v=(1,±1),當l斜率不存在時，不失一般性，取A[,-1],B[,1],則在v上的投影的絕對值為||cos45°=2×,不合題意 

所以l的斜率k存在，其方程為y=k(x-).

由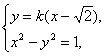得(k²-1)x²-2k²x+2k²+1=0(k²≠1)

設A(x₁,k(x₁-))、B(x₂,k(x₂-)),則

x₁+x₂=,x₁x₂=.

當v=(1,1)時，設與v的夾角為θ,則

=[x₂-x₁,k(x₂-x₁)]在v上投影的絕對值

|||cosθ|=||

=

=.

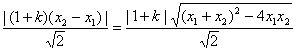
由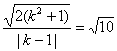,得2k²-5k+2=0,k=2或k= 

根據(jù)雙曲線的對稱性知，當

v=(1,-1)時，k=-2或k=-.

所以直線l的方程為

y=±2(x-)或y=±(x-).