Question

（本小題滿分13分）設向量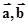滿足及
(1)求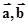夾角的大小；　　　(2)求的值．

Answer 1

(1).(2)|3a＋b|＝.

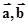解析試題分析：(1)根據(3a－2b)²＝7,9|a|²＋4|b|²－12a·b＝7,可得a·b＝,再根據數量積的定義可求出cos θ＝,進而得到夾角.
(2)先求(3a＋b)²＝9|a|²＋6a·b＋|b|²＝9＋3＋1＝13，從而得到|3a＋b|＝.
(1)設a與b夾角為θ，(3a－2b)²＝7,9|a|²＋4|b|²－12a·b＝7，而|a|＝|b|＝1，
∴a·b＝，∴|a||b|cos θ＝，即cos θ＝
又θ∈[0，π]，∴a，b所成的角為.
(2)(3a＋b)²＝9|a|²＋6a·b＋|b|²＝9＋3＋1＝13，
∴|3a＋b|＝..
考點：考查了向量的數量積，以及利用數量積求模，夾角等知識.
點評：掌握數量積的定義：,
求模可利用:來求解.