
 (a,b為實常數).
(a,b為實常數). ,將2x看成整體,利用其范圍結合不等式的性質即可求得函數f(x)的值域.
,將2x看成整體,利用其范圍結合不等式的性質即可求得函數f(x)的值域. ,
, ,
, ,
, 對任意實數x成立. (6分)
對任意實數x成立. (6分) ,所以
,所以 (舍)或
(舍)或 . (10分)
. (10分) ,
, ,從而
,從而 ; (14分)
; (14分) 對任何實數c成立; (16分)
對任何實數c成立; (16分) ,因為2x>0,(12分)
,因為2x>0,(12分) ,(14分)
,(14分) ;所以函數f(x)的值域為
;所以函數f(x)的值域為 . (18分)
. (18分)

 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:解答題
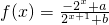 (a,b為實常數).
(a,b為實常數).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
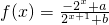 (a,b為實常數).
(a,b為實常數).查看答案和解析>>
科目:高中數學 來源:2011-2012學年吉林省延邊州汪清六中高三(上)第一次月考數學試卷(理科)(解析版) 題型:解答題
 (a,b為實常數).
(a,b為實常數).查看答案和解析>>
科目:高中數學 來源:2012-2013學年新課標高三(上)數學一輪復習單元驗收2(文科)(解析版) 題型:解答題
 (a,b為實常數).
(a,b為實常數).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com