中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知數列滿足,我們知道當a取不同的值時，得到不同的數列，如當時，得到無窮數列：當時,得到有窮數列：.

（Ⅰ）求當為何值時；

（Ⅱ）設數列滿足, ，求證：取數列中的任一個數，都可以得到一個有窮數列；

（Ⅲ）若，求的取值范圍.

（Ⅰ）當為何值時

         (Ⅱ)證明略

        （Ⅲ）


解析:

（Ⅰ）

 

(Ⅱ) 解法一：,,

當時, ,

當時,,,

當時,,.

一般地, 當時,可得一個含有項的有窮數列.

下面用數學歸納法證明.

(1)當時, ,顯然,可得一個含有2項的有窮數列

(2)假設當時,,得到一個含有項的有窮數列,其中

,則時,,,

     由假設可知, 得到一個含有項的有窮數列,其中.

所以,當時, 可以得到一個含有項的有窮數列,,其中

由(1),(2)知,對一切,命題都成立.

解法二：

故取數列中的任一個數，都可以得到一個有窮數列.

（Ⅲ）即,

所以要使,當且僅當它的前一項滿足.

由于,所以只須當時,都有

由,得, 解得.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：閱讀理解

閱讀下面一段文字：已知數列{an}的首項a1=1，如果當n≥2時，an-an-1=2，則易知通項an=2n-1，前n項的和Sn=n2．將此命題中的“等號”改為“大于號”，我們得到：數列{an}的首項a1=1，如果當n≥2時，an-an-1＞2，那么an＞2n-1，且Sn＞n2．這種從“等”到“不等”的類比很有趣．由此還可以思考：要證Sn＞n2，可以先證an＞2n-1，而要證an＞2n-1，只需證an-an-1＞2（n≥2）．結合以上思想方法，完成下題：
已知函數f（x）=x3+1，數列{an}滿足a1=1，an+1=f（an），若數列{an}的前n項的和為Sn，求證：Sn≥2n-1．

查看答案和解析>>

科目：高中數學 來源：2011-2012學年山東省高考模擬預測數學文試卷（解析版） 題型：解答題

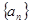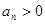已知數列滿足且對一切,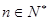

有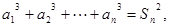

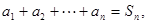
（Ⅰ）求證：對一切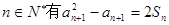

（Ⅱ）求數列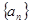通項公式.   

（Ⅲ）求證：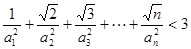

【解析】第一問利用，已知表達式，可以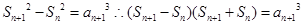得到，然后得到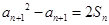，從而求證 。

第二問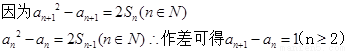，可得數列的通項公式。

第三問中，利用放縮法的思想，我們可以得到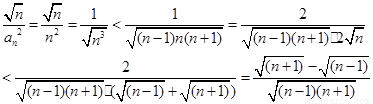

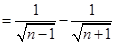然后利用累加法思想求證得到證明。

解:  (1) 證明:

 

 

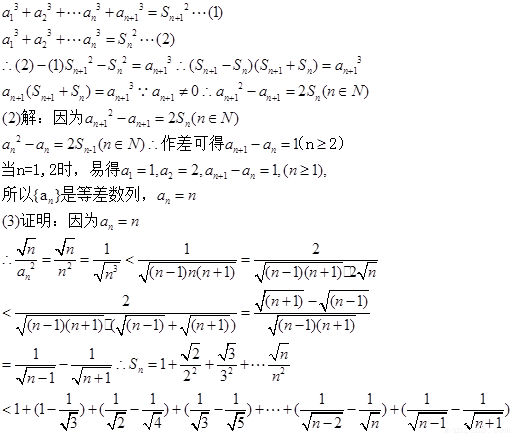
查看答案和解析>>

科目：高中數學 來源：不詳 題型：解答題

閱讀下面一段文字：已知數列{an}的首項a1=1，如果當n≥2時，an-an-1=2，則易知通項an=2n-1，前n項的和Sn=n2．將此命題中的“等號”改為“大于號”，我們得到：數列{an}的首項a1=1，如果當n≥2時，an-an-1＞2，那么an＞2n-1，且Sn＞n2．這種從“等”到“不等”的類比很有趣．由此還可以思考：要證Sn＞n2，可以先證an＞2n-1，而要證an＞2n-1，只需證an-an-1＞2（n≥2）．結合以上思想方法，完成下題：
已知函數f（x）=x3+1，數列{an}滿足a1=1，an+1=f（an），若數列{an}的前n項的和為Sn，求證：Sn≥2n-1．

查看答案和解析>>

科目：高中數學 來源： 題型：閱讀理解

（本小題滿分14分）

閱讀下面一段文字：已知數列的首項，如果當時，，則易知通項，前項的和. 將此命題中的“等號”改為“大于號”，我們得到：數列的首項，如果當時，，那么，且. 這種從“等”到“不等”的類比很有趣。由此還可以思考：要證，可以先證，而要證，只需證（）. 結合以上思想方法，完成下題：

已知函數，數列滿足，，若數列的前項的和為，求證：.

查看答案和解析>>

科目：高中數學 來源：2009-2010學年湖北省部分重點中學聯考高一（下）期中數學試卷（解析版） 題型：解答題

閱讀下面一段文字：已知數列{an}的首項a1=1，如果當n≥2時，an-an-1=2，則易知通項an=2n-1，前n項的和Sn=n2．將此命題中的“等號”改為“大于號”，我們得到：數列{an}的首項a1=1，如果當n≥2時，an-an-1＞2，那么an＞2n-1，且Sn＞n2．這種從“等”到“不等”的類比很有趣．由此還可以思考：要證Sn＞n2，可以先證an＞2n-1，而要證an＞2n-1，只需證an-an-1＞2（n≥2）．結合以上思想方法，完成下題：
已知函數f（x）=x3+1，數列{an}滿足a1=1，an+1=f（an），若數列{an}的前n項的和為Sn，求證：Sn≥2n-1．

查看答案和解析>>

同步練習冊答案