
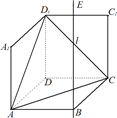
 如圖1,在平面內,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.將兩個正方形分別沿AD,CD折起,使D′′與D′重合于點D1.設直線l過點B且垂直于菱形ABCD所在的平面,點E是直線l上的一個動點,且與點D1位于平面ABCD同側(圖2).
如圖1,在平面內,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.將兩個正方形分別沿AD,CD折起,使D′′與D′重合于點D1.設直線l過點B且垂直于菱形ABCD所在的平面,點E是直線l上的一個動點,且與點D1位于平面ABCD同側(圖2).| π |
| 4 |
| π |
| 3 |
| D1P |
| PE |
| D1P |
| PE |
| π |
| 4 |
| π |
| 3 |
| D1P |
| PE |
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
| a |
| 2 |
| AD1 |
| ||
| 2 |
| a |
| 2 |
| AC |
| 3 |
| n1 |
|
|
|
| n1 |
| AE |
| ||
| 2 |
| a |
| 2 |
| n2 |
|
|
|
| n2 |
| 2t |
| a |
| ||||
|
|
| 4t-a | ||
|
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 4t-a | ||
|
| ||
| 2 |
8+5
| ||
| 22 |
| 3a |
| 2 |
8+5
| ||
| 22 |
| 3a |
| 2 |
| D1P |
| PE |
| a |
| 2 |
| λ-1 |
| λ+1 |
| λt+a |
| 1+λ |
| ||
| 2 |
| A1P |
| ||
| 2 |
| a |
| 2 |
| λ-1 |
| λ+1 |
| λt-aλ |
| 1+λ |
| A1P |
| n2 |
| λ-1 |
| λ+1 |
| λt-aλ |
| 1+λ |
| t |
| a |
| D1P |
| PE |
| BE |
| a |
| D1P |
| PE |
| D1P |
| PE |


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
| π |
| 4 |
| π |
| 3 |
| D1E |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省杭州市高三第二次教學質量考試數學理卷 題型:解答題
(本題滿分14分)
如圖1,在平面內,ABCD是 的菱形,ADD``A1和CD D`C1都是正方形.將兩個正方形分別沿AD,CD折起,使D``與D`重合于點D1 .設直線l過點B且垂直于菱形ABCD所在的平面,點E是直線l上的一個動點,且與點D1位于平面ABCD同側(圖2).
的菱形,ADD``A1和CD D`C1都是正方形.將兩個正方形分別沿AD,CD折起,使D``與D`重合于點D1 .設直線l過點B且垂直于菱形ABCD所在的平面,點E是直線l上的一個動點,且與點D1位于平面ABCD同側(圖2).


(Ⅰ) 設二面角E – AC – D1的大小為q,若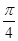 £ q £
£ q £  ,求線段BE長的取值范圍;
,求線段BE長的取值范圍;
(Ⅱ)在線段 上存在點
上存在點 ,使平面
,使平面 平面
平面 ,求
,求 與BE之間滿足的關系式,并證明:當0 < BE < a時,恒有
與BE之間滿足的關系式,并證明:當0 < BE < a時,恒有 <
1.
<
1.
查看答案和解析>>
科目:高中數學 來源: 題型:
己知在銳角ΔABC中,角![]() 所對的邊分別為
所對的邊分別為![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.

20.如圖1,在平面內,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,將
是正三角形,將![]() 沿
沿![]() 折起,使
折起,使![]() 如圖2,
如圖2,![]() 為
為![]() 的中點,設直線
的中點,設直線![]() 過點
過點![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,點
所在平面,點![]() 是直線
是直線![]() 上的一個動點,且與點
上的一個動點,且與點![]() 位于平面
位于平面![]() 的同側。
的同側。
(1)求證:![]() 平面
平面![]() ;
;
(2)設二面角![]() 的平面角為
的平面角為![]() ,若
,若![]() ,求線段
,求線段![]() 長的取值范圍。
長的取值范圍。


21.已知A,B是橢圓![]() 的左,右頂點,
的左,右頂點,![]() ,過橢圓C的右焦點F的直線交橢圓于點M,N,交直線
,過橢圓C的右焦點F的直線交橢圓于點M,N,交直線![]() 于點P,且直線PA,PF,PB的斜率成等差數列,R和Q是橢圓上的兩動點,R和Q的橫坐標之和為2,RQ的中垂線交X軸于T點
于點P,且直線PA,PF,PB的斜率成等差數列,R和Q是橢圓上的兩動點,R和Q的橫坐標之和為2,RQ的中垂線交X軸于T點
(1)求橢圓C的方程;
 (2)求三角形MNT的面積的最大值
(2)求三角形MNT的面積的最大值
22. 已知函數![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值與最小值,且其最大值與最小值的和為
上存在最大值與最小值,且其最大值與最小值的和為![]() ,試求
,試求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 為奇函數:
為奇函數:
(1)是否存在實數![]() ,使得
,使得![]() 在
在![]() 為增函數,
為增函數,![]() 為減函數,若存在,求出
為減函數,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(2)如果當![]() 時,都有
時,都有![]() 恒成立,試求
恒成立,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011年浙江省杭州市高考數學二模試卷(理科)(解析版) 題型:解答題
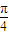 ≤θ≤
≤θ≤ ,求線段BE長的取值范圍;
,求線段BE長的取值范圍; 與BE之間滿足的關系式,并證明:當0<BE<a時,恒有
與BE之間滿足的關系式,并證明:當0<BE<a時,恒有 <1.
<1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com