
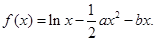
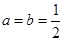 時,求函數
時,求函數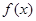 的最大值;
的最大值;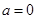 ,
,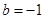 ,方程
,方程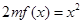 有唯一實數解,求正數
有唯一實數解,求正數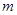 的值.
的值.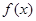 的極大值為
的極大值為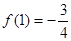 ,此即為最大值;(2)
,此即為最大值;(2) 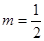 。
。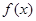 的定義域為(0,+∞),當
的定義域為(0,+∞),當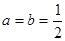 時,
時, ,
,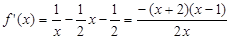 ……………2分
……………2分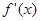 =0,解得
=0,解得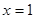 .(∵
.(∵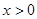 )
)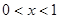 時,
時,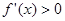 ,此時
,此時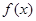 單調遞增;當
單調遞增;當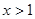 時,
時,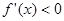 ,此時
,此時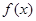 單調遞減.
單調遞減.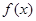 的極大值為
的極大值為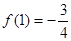 ,此即為最大值 ……………4分
,此即為最大值 ……………4分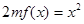 有唯一實數解,所以
有唯一實數解,所以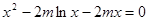 有唯一實數解,
有唯一實數解,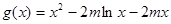 ,則
,則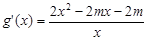 .令
.令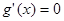 ,
,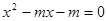 .
. 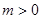 ,
,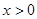 , 所以
, 所以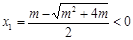 (舍去),
(舍去),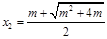 ,…… 6分
,…… 6分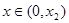 時,
時,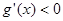 ,
,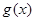 在(0,
在(0,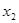 )上單調遞減,
)上單調遞減,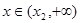 時,
時,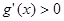 ,
,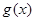 在(
在(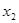 ,+∞)單調遞增
,+∞)單調遞增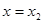 時,
時,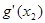 =0,
=0,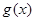 取最小值
取最小值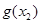 .
. 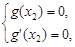 既
既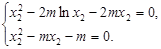 ……………10分
……………10分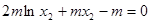 ,因為
,因為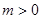 ,所以
,所以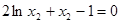 (*)
(*)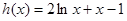 ,因為當
,因為當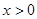 時,
時,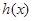 是增函數,所以
是增函數,所以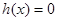 至多有一解.
至多有一解.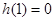 ,所以方程(*)的解為
,所以方程(*)的解為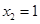 ,即
,即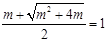 ,解得
,解得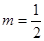 ………12分
………12分

 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com