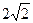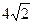(本小題滿分13分)
設(shè)橢圓

過(guò)點(diǎn)

,且著焦點(diǎn)為

(Ⅰ)求橢圓

的方程;
(Ⅱ)當(dāng)過(guò)點(diǎn)

的動(dòng)直線

與橢圓

相交與兩不同點(diǎn)

時(shí),在線段

上取點(diǎn)

,滿足

,證明:點(diǎn)

總在某定直線上
(Ⅰ)

(Ⅱ)見(jiàn)解析
(1)由題意:

,解得

,所求橢圓方程為

(2)方法一
設(shè)點(diǎn)Q、A、B的坐標(biāo)分別為

。
由題設(shè)知

均不為零,記

,則

且

又A,P,B,Q四點(diǎn)共線,從而

于是

,


,

從而

,
(1)

,
(2)
又點(diǎn)A、B在橢圓C上,即


(1)+(2)×2并結(jié)合(3),(4)得

即點(diǎn)

總在定直線

上
方法二
設(shè)點(diǎn)

,由題設(shè),

均不為零。
且
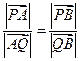
又

四點(diǎn)共線,可設(shè)

,于是

(1)

(2)
由于

在橢圓C上,將(1),(2)分別代入C的方程

整理得
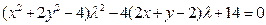
(3)
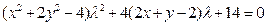
(4)
(4)-(3) 得


即點(diǎn)

總在定直線

上
練習(xí)冊(cè)系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:解答題
已知橢圓

的左焦點(diǎn)到直線

的距離為

,求橢圓的方程。
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:解答題
(本題滿分12分) 直角三角形
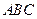
的直角頂點(diǎn)
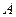
為動(dòng)點(diǎn),
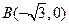
,
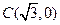
為兩個(gè)定點(diǎn),作
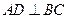
于
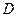
,動(dòng)點(diǎn)
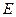
滿足
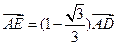
,當(dāng)點(diǎn)
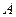
運(yùn)動(dòng)時(shí),設(shè)點(diǎn)
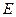
的軌跡為曲線
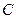
,曲線
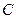
與
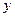
軸正半軸的交點(diǎn)為
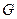
.(Ⅰ) 求曲線
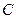
的方程;(Ⅱ) 是否存在方向向量為
m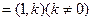
的直線
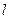
,與曲線
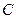
交于
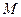
,
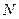
兩點(diǎn),使
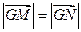
,且
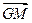
與
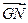
的夾角為
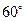
?若存在,求出所有滿足條件的直線方程;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:解答題
若點(diǎn)
P到定點(diǎn)(0,10)與到定直線
y =
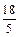
的距離之比是
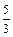
,則點(diǎn)
P的軌跡方程是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:單選題
正四面體P-ABC中,點(diǎn)M在面PBC內(nèi),且點(diǎn)M到點(diǎn)P的距離等于點(diǎn)M到底面ABC的距離則動(dòng)點(diǎn)M在面PBC的軌跡是( )
| A.拋物線的一部分 | B.橢圓的一部分 |
| C.雙曲線的一部分 | D.圓的一部分 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:單選題
△ABC的頂點(diǎn)A(-5,0)、B(5,0),△ABC的周長(zhǎng)為22,則頂點(diǎn)C的軌跡方程是( )
| A.+=1 | B.+=1 |
| C.+=1(y≠0) | D.+=1(y≠0) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:單選題
已知焦點(diǎn)在x軸上的橢圓,長(zhǎng)軸長(zhǎng)為4,右焦點(diǎn)到右頂點(diǎn)的距離為1,則橢圓的標(biāo)準(zhǔn)方程為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:單選題
若方程
+=1表示橢圓,則實(shí)數(shù)k的取值范圍是( )
| A.k<2 | B.k>3 |
| C.2<k<3且k≠ | D.k<2或k>3 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:不詳
題型:單選題
設(shè)
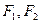
是橢圓
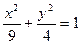
的兩個(gè)焦點(diǎn),
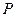
是橢圓上的點(diǎn),且
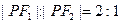
,則
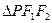
的面積為( )
| A.4 | B. 6 | C.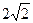 | D.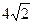 |
查看答案和解析>>

 過(guò)點(diǎn)
過(guò)點(diǎn) ,且著焦點(diǎn)為
,且著焦點(diǎn)為
 的方程;
的方程; 的動(dòng)直線
的動(dòng)直線 與橢圓
與橢圓 相交與兩不同點(diǎn)
相交與兩不同點(diǎn) 時(shí),在線段
時(shí),在線段 上取點(diǎn)
上取點(diǎn) ,滿足
,滿足 ,證明:點(diǎn)
,證明:點(diǎn) 總在某定直線上
總在某定直線上
 ,解得
,解得 ,所求橢圓方程為
,所求橢圓方程為
 。
。 均不為零,記
均不為零,記 ,則
,則 且
且

 ,
, 
 ,
, 
 ,
,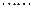 (1)
(1)  ,
,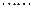 (2)
(2)


 總在定直線
總在定直線 上
上 ,由題設(shè),
,由題設(shè), 均不為零。
均不為零。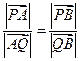
 四點(diǎn)共線,可設(shè)
四點(diǎn)共線,可設(shè) ,于是
,于是 (1)
(1) (2)
(2) 在橢圓C上,將(1),(2)分別代入C的方程
在橢圓C上,將(1),(2)分別代入C的方程 整理得
整理得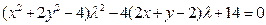 (3)
(3)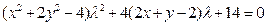 (4)
(4)

 總在定直線
總在定直線 上
上


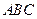 的直角頂點(diǎn)
的直角頂點(diǎn)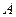 為動(dòng)點(diǎn),
為動(dòng)點(diǎn),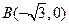 ,
,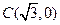 為兩個(gè)定點(diǎn),作
為兩個(gè)定點(diǎn),作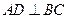 于
于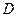 ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)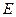 滿足
滿足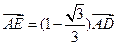 ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)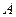 運(yùn)動(dòng)時(shí),設(shè)點(diǎn)
運(yùn)動(dòng)時(shí),設(shè)點(diǎn)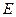 的軌跡為曲線
的軌跡為曲線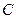 ,曲線
,曲線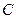 與
與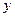 軸正半軸的交點(diǎn)為
軸正半軸的交點(diǎn)為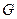 .(Ⅰ) 求曲線
.(Ⅰ) 求曲線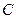 的方程;(Ⅱ) 是否存在方向向量為m
的方程;(Ⅱ) 是否存在方向向量為m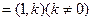 的直線
的直線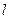 ,與曲線
,與曲線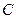 交于
交于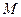 ,
,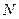 兩點(diǎn),使
兩點(diǎn),使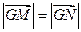 ,且
,且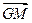 與
與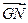 的夾角為
的夾角為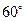 ?若存在,求出所有滿足條件的直線方程;若不存在,說(shuō)明理由.
?若存在,求出所有滿足條件的直線方程;若不存在,說(shuō)明理由.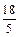 的距離之比是
的距離之比是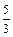 ,則點(diǎn)P的軌跡方程是( )
,則點(diǎn)P的軌跡方程是( )

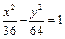

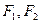 是橢圓
是橢圓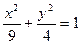 的兩個(gè)焦點(diǎn),
的兩個(gè)焦點(diǎn),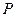 是橢圓上的點(diǎn),且
是橢圓上的點(diǎn),且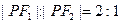 ,則
,則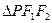 的面積為( )
的面積為( )