(本題滿分16分)已知橢圓
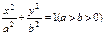
的離心率為
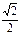
.
⑴若圓(x-2)
2+(y-1)
2=
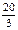
與橢圓相交于A、B兩點且線段AB恰為圓的直徑,求橢圓W方程;
⑵設L為過橢圓右焦點F的直線,交橢圓于M、N兩點,且L的傾斜角為60
0.求
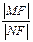
的值.
⑶在(1)的條件下,橢圓W的左右焦點分別為F
1、 F
2,點R在直線l:x-

y+8=0上.當∠F
1RF
2取最大值時,求
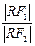
的值.
解:(1)設A(x
1,y
1),B(x
2,y
2),AB的方程為y-1="k(x-2)" 即y=kx+1-2k①
∵離心率e=
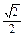
∴橢圓方程可化為
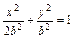
②
將①代入②得(1+2k
2)x
2+4(1-2k)·kx
+2(1-2k)
2-2b
2=0
∵x
1+x
2=
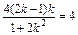
∴k=-1
∴x
1x
2=
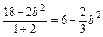
又
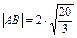
∴
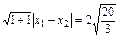
即
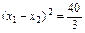
∴b
2="8 "
∴橢圓方程為
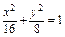
(2)設
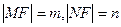
,則由第二定義知
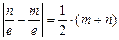
即
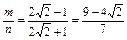
或
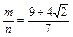
∴
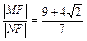
或
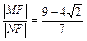
.
(3)當∠F
1RF
2取最大值時,過R、F
1、F
2的圓的圓心角最大,故其半徑最小,與直線l相切.
直線l與x軸于S(-8,0),
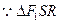
∽
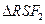
(可證)
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設橢圓
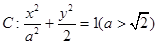
的左右焦點分別為F
1,F(xiàn)
2,A是橢圓C上第一象限內一點,
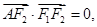
坐標原點O到直線AF
1的距離為
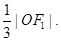
(I)求橢圓C的方程;
(II)設Q是橢圓C上的一點,過點Q的直線
l交
x軸于點
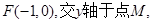
若
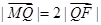
,求直線
l的斜率。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知
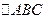
的兩個頂點
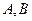
的坐標為
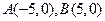
,且
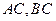
的斜率之積等于
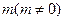
,若頂點
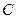
的軌跡是雙曲線(去掉兩個頂點),求
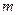
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若雙曲線
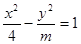
的漸近線方程為
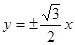
,則雙曲線的焦點坐標是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
“雙曲線方程為
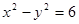
”是“雙曲線離心率
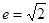
”的 ( )
| A.充要條件 | B.充分不必要條件 |
| C.必要不充分條件 | D.既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
橢圓
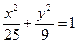
的左、右焦點為
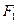
、
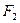
,
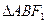
的頂點A、B在橢圓上,且邊AB經(jīng)過右焦點
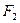
,則
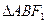
的周長是_________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
直線y=x+b與曲線x=
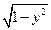
恰有一個交點,則實數(shù)的b的取值范圍是__________
查看答案和解析>>

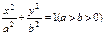 的離心率為
的離心率為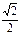 .
.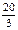 與橢圓相交于A、B兩點且線段AB恰為圓的直徑,求橢圓W方程;
與橢圓相交于A、B兩點且線段AB恰為圓的直徑,求橢圓W方程;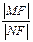 的值.
的值. y+8=0上.當∠F1RF2取最大值時,求
y+8=0上.當∠F1RF2取最大值時,求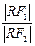 的值.
的值. 智能訓練練測考系列答案
智能訓練練測考系列答案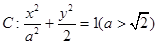 的左右焦點分別為F1,F(xiàn)2,A是橢圓C上第一象限內一點,
的左右焦點分別為F1,F(xiàn)2,A是橢圓C上第一象限內一點,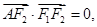 坐標原點O到直線AF1的距離為
坐標原點O到直線AF1的距離為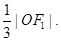
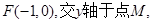 若
若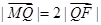 ,求直線l的斜率。
,求直線l的斜率。