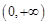中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
下列函數中,在區間上為增函數的是
A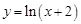．B．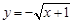
C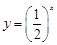．D．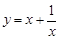
A

試題分析： 因為選項A中，現看定義域x>-2,且是一個復合函數，內層是一次遞增函數，外層是遞增的自然對數函數y=lnx，那么利用同增異減來判定，選項A成立。
選項B中，由于定義域x-1，同時因為y=是遞增函數，那么則可知是遞減函數。錯誤
選項C中，表示的為底數小于1的指數函數，因此是單調遞減函數，錯誤。而選項D中，由于，可見增區間為x>1,故錯誤，選A.
點評：解決該試題的關鍵是能利用對數函數與指數函數單調性的底數的范圍來確定處增減性，同時能根據導數的思想來證明對勾函數的單調性。
練習冊系列答案
相關習題

科目：高中數學 來源：不詳 題型：解答題

(本小題滿分12分)
某工廠修建一個長方體無蓋蓄水池，其容積為4800立方米，深度為3米．池底每平方米的 造價為150元，池壁每平方米的造價為120元．設池底長方形長為米．
(1)求底面積，并用含的表達式表示池壁面積；
(2)怎樣設計水池能使總造價最低?最低造價是多少?

查看答案和解析>>

科目：高中數學 來源：不詳 題型：單選題

設f(x)是R上的奇函數，且當x>0時,f(x)=x(1+),則當x<0時,f(x)=(    )
A．-x(1+)B．x(1+)C．-x(1-)D． x(1-)

查看答案和解析>>

科目：高中數學 來源：不詳 題型：填空題

已知函數,滿足,,,,則函數的圖象在處的切線方程為        .

查看答案和解析>>

科目：高中數學 來源：不詳 題型：解答題

（本小題滿分12）
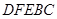為了綠化城市，準備在如圖所示的區域內修建一個矩形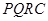的草坪，并建立如圖平面直角坐標系，且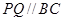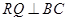，，另外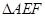的內部有一文物保護區不能占用，經測量，, ,.
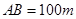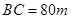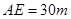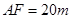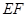（1）求直線的方程；
（2）應如何設計才能使草坪的占地面積最大？并求最大面積。

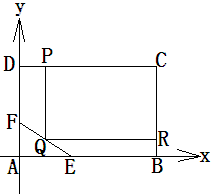
查看答案和解析>>

科目：高中數學 來源：不詳 題型：填空題

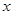關于的方程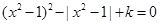，給出下列四個題：
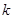①存在實數，使得方程恰有2個不同的實根；
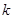②存在實數，使得方程恰有4個不同的實根；
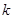③存在實數，使得方程恰有5個不同的實根；
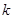④存在實數，使得方程恰有8個不同的實根。
正確命題的序號為           

查看答案和解析>>

科目：高中數學 來源：不詳 題型：單選題

具有性質：的函數，我們稱為滿足“倒負”變換的函數，下列函數：①；②；③中滿足“倒負”變換的函數是（  ）
A．①②B．①③C．②③D．只有①

查看答案和解析>>

科目：高中數學 來源：不詳 題型：填空題

設函數對任意滿足，且，則的值為     。 

查看答案和解析>>

科目：高中數學 來源：不詳 題型：單選題

已知，，，
若函數不存在零點，則的范圍是 （     ）
A．B．C．D．

查看答案和解析>>

同步練習冊答案