
(本小題共14分)
為預防![]() 病毒暴發(fā),某生物技術公司研制出一種新流感疫苗,為測試該疫苗的有效性(若疫苗有效的概率小于90%,則認為測試沒有通過),公司選定2000個流感樣本分成三組,測試結果如下表:
病毒暴發(fā),某生物技術公司研制出一種新流感疫苗,為測試該疫苗的有效性(若疫苗有效的概率小于90%,則認為測試沒有通過),公司選定2000個流感樣本分成三組,測試結果如下表:
| A組 | B組 | C組 | |
| 疫苗有效 | 673 |
|
|
| 疫苗無效 | 77 | 90 |
|
已知在全體樣本中隨機抽取1個,抽到B組疫苗有效的概率是0.33.
(1)求![]() 的值;
的值;
(2)現(xiàn)用分層抽樣的方法在全體樣本中抽取360個測試結果,問應在C組抽取多少個?
(3)已知![]() ,求不能通過測試的概率.
,求不能通過測試的概率.
(本小題共14分)
解:(1)![]() 在全體樣本中隨機抽取1個,抽到B組疫苗有效的概率約為其頻率
在全體樣本中隨機抽取1個,抽到B組疫苗有效的概率約為其頻率
即![]()
![]()
![]() …………………………(4分)
…………………………(4分)
(2)C組樣本個數(shù)為y+z=2000-(673+77+660+90)=500,
現(xiàn)用分層抽樣的方法在全體樣本中抽取360個測試結果,
則![]() ………………………………(7分)
………………………………(7分)
答:應在C組抽取個數(shù)為90.……………………………………………………8分
(3)設測試不能通過事件為A ,C組疫苗有效與無效的可能的情況記為(y,z) 由(2)知 ![]() ,且
,且 ![]() ,基本事件空間包含的基本事件有:
,基本事件空間包含的基本事件有:
(465,35)、(466,34)、(467,33)、……(475,25)共11個 …………… (11分)
若測試不能通過,則77+90+z>200,即z>33
事件A包含的基本事件有:((465,35)、(466,34)共2個
![]()
![]() …………………(13分)
…………………(13分)
故不能通過測試的概率為![]() …………………(14分)
…………………(14分)


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數(shù)學 來源: 題型:
(本小題共14分)
數(shù)列![]() 的前n項和為
的前n項和為![]() ,點
,點![]() 在直線
在直線![]()
上.
(I)求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(II)若數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的前n項和
的前n項和![]()
(III)設![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本小題共14分)
如圖,四棱錐![]() 的底面是正方形,
的底面是正方形,![]() ,點E在棱PB上。
,點E在棱PB上。

(Ⅰ)求證:平面![]() ;
;
(Ⅱ)當![]() 且E為PB的中點時,求AE與平面PDB所成的角的大小。
且E為PB的中點時,求AE與平面PDB所成的角的大小。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(2009北京理)(本小題共14分)
已知雙曲線![]() 的離心率為
的離心率為![]() ,右準線方程為
,右準線方程為![]()
(Ⅰ)求雙曲線![]() 的方程;
的方程;
(Ⅱ)設直線![]() 是圓
是圓![]() 上動點
上動點![]() 處的切線,
處的切線,![]() 與雙曲線
與雙曲線![]() 交
交
于不同的兩點![]() ,證明
,證明![]() 的大小為定值.
的大小為定值.
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆度廣東省高二上學期11月月考理科數(shù)學試卷 題型:解答題
(本小題共14分)在四棱錐P-ABCD中,底面ABCD是正方形,側棱PD 底面ABCD,PD=DC,點E是PC的中點,作EF
底面ABCD,PD=DC,點E是PC的中點,作EF PB交PB于點F
PB交PB于點F
⑴求證:PA//平面EDB
⑵求證:PB 平面EFD
平面EFD
⑶求二面角C-PB-D的大小

查看答案和解析>>
科目:高中數(shù)學 來源:2010年北京市崇文區(qū)高三下學期二模數(shù)學(文)試題 題型:解答題
(本小題共14分)
正方體 的棱長為
的棱長為 ,
, 是
是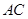 與
與 的交點,
的交點, 為
為 的中點.
的中點.
(Ⅰ)求證:直線 ∥平面
∥平面 ;
;
(Ⅱ)求證: 平面
平面 ;
;
(Ⅲ)求三棱錐 的體積.
的體積.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com