
在銳角△ABC中,角A,B,C的對邊分別為a,b,c.已知sin(A-B)=cosC.
(1)若a=3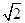 ,b=
,b=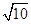 ,求c;
,求c;
(2)求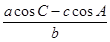 的取值范圍.
的取值范圍.
(1)c=4(2)(-1,1)
解析試題分析:(1)由cosC=sin( -C).結合條件可得A-B+C=
-C).結合條件可得A-B+C= ,從而B=
,從而B= ,再利用余弦定理求出c;
,再利用余弦定理求出c;
(2)結合B= ,利用正弦定理和兩角差的正弦將原式化為
,利用正弦定理和兩角差的正弦將原式化為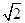 sin(2A-
sin(2A- ),由A的范圍可得原式的范圍.
),由A的范圍可得原式的范圍.
試題解析:解:(1)由sin(A-B)=cosC,得sin(A-B)=sin( -C).
-C).
∵△ABC是銳角三角形,∴A-B= -C,即A-B+C=
-C,即A-B+C= ,①
,①
又A+B+C=π,②由②-①,得B= .
.
由余弦定理b2=c2+a2-2cacosB,得(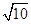 )2=c2+(3
)2=c2+(3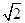 )2-2c×3
)2-2c×3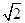 cos
cos ,
,
即c2-6c+8=0,解得c=2,或c=4.
當c=2時,b2+c2-a2=(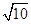 )2+22-(3
)2+22-(3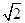 )2=-4<0,
)2=-4<0,
∴b2+c2<a2,此時A為鈍角,與已知矛盾,∴c≠2.
故c=4. 6分
(2)由(1),知B= ,∴A+C=
,∴A+C= ,即C=
,即C= -A.
-A.
∴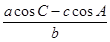 =
= =
= =
=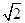 sin(2A-
sin(2A- ).
).
∵△ABC是銳角三角形,∴
 <A<
<A< ,∴-
,∴- <2A-
<2A- <
< ,
,
∴- <sin(2A-
<sin(2A- )<
)< ,∴-1<
,∴-1<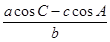 <1.
<1.
故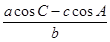 的取值范圍為(-1,1). 12分
的取值范圍為(-1,1). 12分
考點:正弦定理,余弦定理,三角函數性質.


科目:高中數學 來源: 題型:解答題
已知角A、B、C為△ABC的三個內角,其對邊分別為a、b、c,若 ,
, ,a=2
,a=2 ,且
,且 ·
· =
=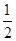 .
.
(1)若△ABC的面積S= ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,漁船甲位于島嶼A的南偏西60°方向的B處,且與島嶼A相距12海里,漁船乙以10海里/時的速度從島嶼A出發沿正北方向航行,若漁船甲同時從B處出發沿北偏東α的方向追趕漁船乙,剛好用2小時追上,此時到達C處.
(1)求漁船甲的速度;
(2)求sinα的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知△ABC的角A、B、C所對的邊分別是a、b、c,設向量m=(a,b),n=(sinB,sinA),p=(b-2,a-2).
(1)若m∥n,求證:△ABC為等腰三角形;
(2)若m⊥p,邊長c=2,角C= ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com