
某校要建一個面積為450平方米的矩形球場,要求球場的一面利用舊墻,其他各面用鋼筋網圍成,且在矩形一邊的鋼筋網的正中間要留一個3米的進出口(如圖).設矩形的長為 米,鋼筋網的總長度為
米,鋼筋網的總長度為 米.
米.
(1)列出 與
與 的函數關系式,并寫出其定義域;
的函數關系式,并寫出其定義域;
(2)問矩形的長與寬各為多少米時,所用的鋼筋網的總長度最小?
(3)若由于地形限制,該球場的長和寬都不能超過25米,問矩形的長與寬各為多少米時,所用的鋼筋網的總長度最小?
(1)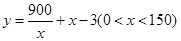
(2)長為30米,寬為15米,所用的鋼筋網的總長度最小.
(3)長為25米,寬為18米時,所用的鋼筋網的總長度最小
解析試題分析:(1)根據矩形的面積求出解析式,注意函數的定義域
(2)利用基本不等式求解,注意等號成立的條件
(3)利用函數的單調性求解(導數或單調性定義)
試題解析:(1)矩形的寬為: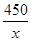 米
米 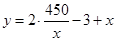
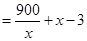
定義域為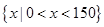
注:定義域為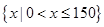 不扣分
不扣分
(2)
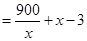
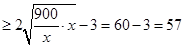
當且僅當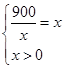 即
即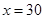 時取等號,此時寬為:
時取等號,此時寬為: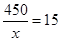 米
米
所以,長為30米,寬為15米,所用的鋼筋網的總長度最小.
(3)法一:
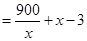
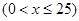 ,
,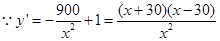
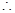 當
當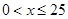 時,
時,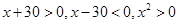
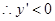
 在
在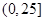 上是單調遞減函數
上是單調遞減函數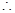 當
當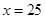 時,
時,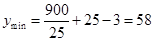 ,此時,長為25米,寬為
,此時,長為25米,寬為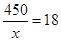 米
米
所以,長為25米,寬為18米時,所用的鋼筋網的總長度最小.
法二:設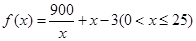 ,
,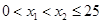 ,
,
則 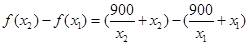
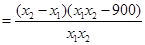
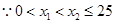 ,
,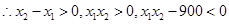
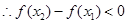 ,
, 
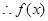 在
在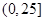 上是單調遞減函數
上是單調遞減函數 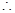 當
當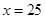 時,
時,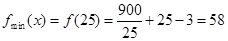
此時,長為25米,寬為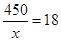 米
米
所以,長為25米,寬為18米時,所用的鋼筋網的總長度最小.
考點:基本不等式的應用,函數的單調性,最值


科目:高中數學 來源: 題型:解答題
已知函數f(x)=3x-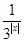 .
.
(1)若f(x)=2,求x的值;
(2)判斷x>0時,f(x)的單調性;
(3)若3tf(2t)+mf(t)≥0對于t∈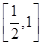 恒成立,求m的取值范圍.
恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數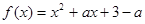 ,
,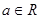 .
.
(1)求 的取值范圍,使
的取值范圍,使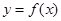 在閉區間
在閉區間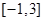 上是單調函數;
上是單調函數;
(2)當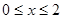 時,函數
時,函數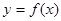 的最大值是關于
的最大值是關于 的函數
的函數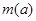 .求
.求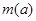 ;
;
(3)求實數 的取值范圍,使得對任意的
的取值范圍,使得對任意的
 ,恒有
,恒有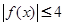 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某通訊公司需要在三角形地帶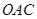 區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域
區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域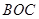 內,乙中轉站建在區域
內,乙中轉站建在區域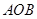 內.分界線
內.分界線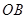 固定,且
固定,且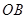 =
=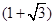 百米,邊界線
百米,邊界線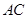 始終過點
始終過點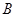 ,邊界線
,邊界線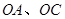 滿足
滿足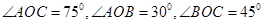 .
.
設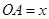 (
(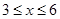 )百米,
)百米,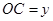 百米.
百米.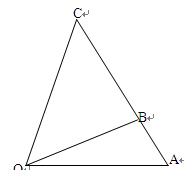
(1)試將 表示成
表示成 的函數,并求出函數
的函數,并求出函數 的解析式;
的解析式;
(2)當 取何值時?整個中轉站的占地面積
取何值時?整個中轉站的占地面積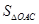 最小,并求出其面積的最小值.
最小,并求出其面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若在定義域存在實數
,若在定義域存在實數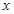 ,滿足
,滿足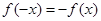 ,則稱
,則稱 為“局部奇函數”.
為“局部奇函數”.
(1)已知二次函數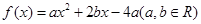 ,試判斷
,試判斷 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)設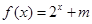 是定義在
是定義在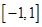 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數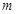 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 的圖象關于坐標原點對稱。
的圖象關于坐標原點對稱。
(1)求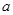 的值,并求出函數
的值,并求出函數 的零點;
的零點;
(2)若函數 在[0,1]內存在零點,求實數b的取值范圍;
在[0,1]內存在零點,求實數b的取值范圍;
(3)設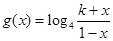 ,已知
,已知 的反函數
的反函數 =
= ,若不等式
,若不等式 在
在 上恒成立,求滿足條件的最小整數k的值。
上恒成立,求滿足條件的最小整數k的值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經市場調查,某種商品在過去50天的銷量和價格均為銷售時間t(天)的函數,且銷售量近似地滿足f(t)=-2t+200(1≤t≤50,t∈N),前30天價格為g(t)= t+30(1≤t≤30,t∈N),后20天價格為g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天價格為g(t)=45(31≤t≤50,t∈N).
(1)寫出該種商品的日銷售額S與時間t的函數關系式;
(2)求日銷售額S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=x2-4,設曲線y=f(x)在點(xn,f(xn))
處的切線與x軸的交點為(xn+1,0)(n∈N+),其中x1為正實數.
(1)用xn表示xn+1;
(2)求證:對一切正整數n,xn+1≤xn的充要條件是x1≥2;
(3)若x1=4,記an=lg  ,證明數列{an}成等比數列,并求數列{xn}的通項公式.
,證明數列{an}成等比數列,并求數列{xn}的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com